题目内容
已知抛物线x2=4y上有一点长为6的弦AB所在直线倾斜角为45°,则AB中点到x轴的距离为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:抛物线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:设A(x1,
x12),B(x2,
x22),由弦AB所在直线倾斜角为45°,可得x1+x2=4,由|AB|=6,可得x1-x2=3
,进而根据AB中点到x轴的距离
=
(x12+x22)=
[(x1+x2)2+(x1-x2)2]得到答案.
| 1 |
| 4 |
| 1 |
| 4 |
| 2 |
| y1+y2 |
| 2 |
| 1 |
| 8 |
| 1 |
| 16 |
解答:
解:设A(x1,
x12),B(x2,
x22)
由弦AB所在直线倾斜角为45°,
可得:kAB=
=
(x1+x2)=1,
则x1+x2=4,
又∵|AB|=6,故x1-x2=3
,
则AB中点到x轴的距离
=
(x12+x22)=
[(x1+x2)2+(x1-x2)2]=
,
故选:D
| 1 |
| 4 |
| 1 |
| 4 |
由弦AB所在直线倾斜角为45°,
可得:kAB=
| ||
| x1-x2 |
| 1 |
| 4 |
则x1+x2=4,
又∵|AB|=6,故x1-x2=3
| 2 |
则AB中点到x轴的距离
| y1+y2 |
| 2 |
| 1 |
| 8 |
| 1 |
| 16 |
| 17 |
| 8 |
故选:D
点评:本题主要考查了抛物线的应用.灵活利用了抛物线的定义.

练习册系列答案
相关题目
已知正四棱锥S-ABCD中,SA=2
,那么当该棱锥的体积最大时,它的底面积为( )
| 3 |
| A、4 | B、8 | C、16 | D、32 |
四面体ABCD中,AD=BC,且AD⊥BC,E、F分别是AB、CD的中点,则EF与BC所成的角为( )
| A、30° | B、45° |
| C、60° | D、90° |
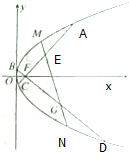 如图,抛物线C:y2=2px(p>0)的焦点F(1,0),过点F任作两条弦AC,BD,且
如图,抛物线C:y2=2px(p>0)的焦点F(1,0),过点F任作两条弦AC,BD,且 如图,边长为2的正方形ACDE所在平面与平面ABC垂直,AD与CE的交点为M,AC⊥BC,且AC=BC,
如图,边长为2的正方形ACDE所在平面与平面ABC垂直,AD与CE的交点为M,AC⊥BC,且AC=BC,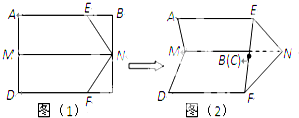 如图(1),矩形ABCD中,M、N分别为边AD、BC的中点,E、F分别为边AB、CD上的定点且满足EB=FC,现沿MN,EN,FN折叠使点B、C重合且与E、F共线,如图(2).若此时二面角A-MN-D的大小为60°,则折叠后EN与平面MNFD所成角的正弦值是( )
如图(1),矩形ABCD中,M、N分别为边AD、BC的中点,E、F分别为边AB、CD上的定点且满足EB=FC,现沿MN,EN,FN折叠使点B、C重合且与E、F共线,如图(2).若此时二面角A-MN-D的大小为60°,则折叠后EN与平面MNFD所成角的正弦值是( )