题目内容
已知一企业生产某产品的年固定成本为10万元,每生产千件该产品需另投入2.7万元,设该企业年内共生产此种产品x千件,并且全部销售完,每千件的销售收入为f(x)万元,且f(x)=
.
(Ⅰ)写出年利润P(万元)关于产品年产量x(千件)的函数关系式;
(Ⅱ)年产量x为多少千件时,该企业生产此产品所获年利润最大?(注:年利润=年销售收入-年总成本)
|
(Ⅰ)写出年利润P(万元)关于产品年产量x(千件)的函数关系式;
(Ⅱ)年产量x为多少千件时,该企业生产此产品所获年利润最大?(注:年利润=年销售收入-年总成本)
考点:函数模型的选择与应用,分段函数的应用
专题:计算题,应用题,函数的性质及应用,导数的综合应用,不等式的解法及应用
分析:(Ⅰ)当0<x≤10时,P=xf(x)-(10+2.7x)=8.1x-
-10;当x>10时,P=xf(x)-(10+2.7x)=98-
-2.7x;写成分段函数即可;
(Ⅱ)分0<x≤10与10<x时讨论函数的最大值,从而求最大值点即可.
| x3 |
| 30 |
| 1000 |
| 3x |
(Ⅱ)分0<x≤10与10<x时讨论函数的最大值,从而求最大值点即可.
解答:
解:(Ⅰ)当0<x≤10时,
P=xf(x)-(10+2.7x)=8.1x-
-10;
当x>10时,P=xf(x)-(10+2.7x)=98-
-2.7x;
故P=
;
(Ⅱ)①当0<x≤10时,由P′=8.1-
=0解得,x=9;
故当x=9时有最大值P=8.1×9-
-10=38.6;
②当10<x时,由P=98-(
+2.7x)≤98-2
=38;
(当且仅当
=2.7x,即x=
时,等号成立);
综上所述,当x=9时,P取得最大值.
即当年产量x为9千件时,该企业生产此产品所获年利润最大.
P=xf(x)-(10+2.7x)=8.1x-
| x3 |
| 30 |
当x>10时,P=xf(x)-(10+2.7x)=98-
| 1000 |
| 3x |
故P=
|
(Ⅱ)①当0<x≤10时,由P′=8.1-
| x2 |
| 10 |
故当x=9时有最大值P=8.1×9-
| 93 |
| 30 |
②当10<x时,由P=98-(
| 1000 |
| 3x |
|
(当且仅当
| 1000 |
| 3x |
| 100 |
| 9 |
综上所述,当x=9时,P取得最大值.
即当年产量x为9千件时,该企业生产此产品所获年利润最大.
点评:本题考查了函数在实际问题中的应用,同时考查了导数的应用与基本不等式的应用,属于中档题.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目
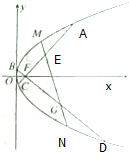 如图,抛物线C:y2=2px(p>0)的焦点F(1,0),过点F任作两条弦AC,BD,且
如图,抛物线C:y2=2px(p>0)的焦点F(1,0),过点F任作两条弦AC,BD,且 如图,边长为2的正方形ACDE所在平面与平面ABC垂直,AD与CE的交点为M,AC⊥BC,且AC=BC,
如图,边长为2的正方形ACDE所在平面与平面ABC垂直,AD与CE的交点为M,AC⊥BC,且AC=BC,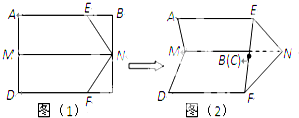 如图(1),矩形ABCD中,M、N分别为边AD、BC的中点,E、F分别为边AB、CD上的定点且满足EB=FC,现沿MN,EN,FN折叠使点B、C重合且与E、F共线,如图(2).若此时二面角A-MN-D的大小为60°,则折叠后EN与平面MNFD所成角的正弦值是( )
如图(1),矩形ABCD中,M、N分别为边AD、BC的中点,E、F分别为边AB、CD上的定点且满足EB=FC,现沿MN,EN,FN折叠使点B、C重合且与E、F共线,如图(2).若此时二面角A-MN-D的大小为60°,则折叠后EN与平面MNFD所成角的正弦值是( )