题目内容
曲线
+
=1与曲线
+
=1(12<k<16)的( )
| x2 |
| 16 |
| y2 |
| 12 |
| x2 |
| 16-x |
| y2 |
| 12-k |
| A、长轴长与实轴长相等 |
| B、短轴长与虚轴长相等 |
| C、焦距相等 |
| D、离心率相等 |
考点:椭圆的简单性质,双曲线的标准方程
专题:圆锥曲线的定义、性质与方程
分析:由曲线的标准方程分别计算其焦距即可判断出.
解答:
解:曲线
+
=1是焦点在x轴上的椭圆,半焦距c1=
=2.
曲线
+
=1(12<k<16)表示焦点在x轴上的双曲线,半焦距c2=
=2.
∴两曲线的截距相等.
故选:C.
| x2 |
| 16 |
| y2 |
| 12 |
| 16-12 |
曲线
| x2 |
| 16-k |
| y2 |
| 12-k |
| 16-k-(12-k) |
∴两曲线的截距相等.
故选:C.
点评:本题考查了标准方程及其性质,属于基础题.

练习册系列答案
相关题目
已知a=log0.70.8,b=20.8,c=log20.9,则( )
| A、a<b<c |
| B、a<c<b |
| C、c<b<a |
| D、c<a<b |
双曲线
-y2=1的离心率的值是( )
| x2 |
| 4 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若0≤x≤2,则f(x)=
的最大值( )
| x(8-3x) |
A、
| ||||
| B、2 | ||||
C、
| ||||
D、
|
函数y=2sin(2x+
)是( )
| π |
| 2 |
| A、周期为π的偶函数 |
| B、周期为π的奇函数 |
| C、周期为2π的偶函数 |
| D、周期为2π的奇函数 |
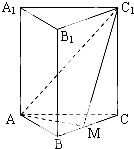 如图,正三棱柱ABC-A1B1C1的底面边长为1,点M在BC上,△AMC1是以M为直角顶点的等腰直角三角形.
如图,正三棱柱ABC-A1B1C1的底面边长为1,点M在BC上,△AMC1是以M为直角顶点的等腰直角三角形.