题目内容
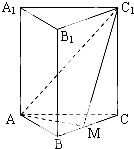 如图,正三棱柱ABC-A1B1C1的底面边长为1,点M在BC上,△AMC1是以M为直角顶点的等腰直角三角形.
如图,正三棱柱ABC-A1B1C1的底面边长为1,点M在BC上,△AMC1是以M为直角顶点的等腰直角三角形.(1)求证:点M为BC的中点;
(2)求点B到平面AMC1的距离;
(3)求二面角M-AC1-C的大小.
考点:二面角的平面角及求法,点、线、面间的距离计算
专题:空间位置关系与距离,空间角
分析:(1)由已知得CC1⊥AM,AM⊥MC1且AM=MC1,从而AM⊥面CC1M,由此能证明点M为BC中点.
(2)法一:过点B作BH⊥C1M,交其延长线于H,则AM⊥C1M,AM⊥CB,从而BH为点B到平面AMC1的距离,由此能求出结果.
法二:设点B到平面AMC1的距离为h.则VB-AMC1=VA-BMC1,由此利用等积法能求出点B到平面AMC1的距离.
(3)法一:过M作MH⊥AC于H,作MG⊥AC1于G,连结GH.,∠MGH为二面角M-AC1-C的平面角,由此能求出二面角M-AC1-C的大小.
法二:过M作MM1∥CC1,交B1C1于M1.以M为坐标原点,BC,AM,MM1分别为x轴,y轴,z轴,利用向量法能求出二面角M-AC1-C的大小.
(2)法一:过点B作BH⊥C1M,交其延长线于H,则AM⊥C1M,AM⊥CB,从而BH为点B到平面AMC1的距离,由此能求出结果.
法二:设点B到平面AMC1的距离为h.则VB-AMC1=VA-BMC1,由此利用等积法能求出点B到平面AMC1的距离.
(3)法一:过M作MH⊥AC于H,作MG⊥AC1于G,连结GH.,∠MGH为二面角M-AC1-C的平面角,由此能求出二面角M-AC1-C的大小.
法二:过M作MM1∥CC1,交B1C1于M1.以M为坐标原点,BC,AM,MM1分别为x轴,y轴,z轴,利用向量法能求出二面角M-AC1-C的大小.
解答:
(1)证明:∵在正三棱柱ABC-A1B1C1中,有CC1⊥底面ABC,AM?面ABC,
∴CC1⊥AM,…(1分)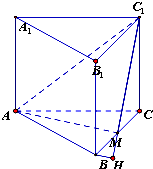
又∵△AMC1是以点M为直角顶点的等腰直角三角形,
∴AM⊥MC1且AM=MC1
∵CC1∩C1M=C1,
∴AM⊥面CC1M,…(2分)
∵BC?面CC1M,
∴AM⊥BC,…(3分)
∵底面ABC是边长为1的正三角形,
∴点M为BC中点.…(4分)
(2)解法一:过点B作BH⊥C1M,交其延长线于H,
由(1)知AM⊥C1M,AM⊥CB,
∴AM⊥平面C1CBB1,
∴AM⊥BH,∴BH⊥平面AMC1,
∴BH为点B到平面AMC1的距离,…(6分)
∴AM=C1M=
,
在Rt△CC1M中,解得CC1=
,…(7分)
∵△BHM∽△C1CM,
∴
=
,∴
=
,
解得BH=
.…(9分)
(2)解法二:设点B到平面AMC1的距离为h.
则VB-AMC1=VA-BMC1,…(5分)
由(I)知 AM⊥C1M,AM⊥CB,
∴AM⊥平面C1CBB1…(6分)
∵AB=1,BM=
,∴AM=MC1=
,CC1=
,…(7分)
∴
S△AMC1•h=
S△C1MB•AM,…(8分)
∴
×
×
×
h=
×
×
×
,
解得h=
.…(9分)
(3)解法一:过M作MH⊥AC于H,作MG⊥AC1于G,连结GH.
∵平面AC1⊥平面ABC,且面AC1∩面ABC=AC,
又MH?面ABC,MH⊥AC,∴MH⊥面AC1,∴MH⊥AC1,
又∵MG⊥AC1,且MH∩MG=M,
∴AC1⊥面MHG,∴AC1⊥GH,
故∠MGH为二面角M-AC1-C的平面角,…(11分)
由(1)知MH=
AM=
,
在等腰直角三角形AMC1中,MG=
AM=
•
=
,
∴sin∠MGH=
=
•
=
.…(13分)
因为二面角M-AC1-C为锐二面角,故∠MGH=
,
所以二面角M-AC1-C的大小为
.…(14分)
(3)解法二:过M作MM1∥CC1,交B1C1于M1.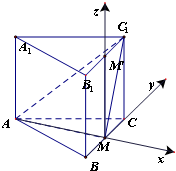
以M为坐标原点,BC,AM,MM1分别为x轴,y轴,z轴,
建立空间直角坐标系.…(10分)
设面ACC1的一个法向量为
=(x,y,z),
则
,取y=1,得
=(-
,1,0),…(11分)
同理可求得面AMC1的一个法向量为
=(-
,0,1),…(12分)
设二面角M-AC1-C的大小为θ,由图知θ为锐角,
故cosθ=|
,
|=
=
,解得θ=
.…(13分)
故二面角M-AC1-C的大小为
.…(14分)
∴CC1⊥AM,…(1分)

又∵△AMC1是以点M为直角顶点的等腰直角三角形,
∴AM⊥MC1且AM=MC1
∵CC1∩C1M=C1,
∴AM⊥面CC1M,…(2分)
∵BC?面CC1M,
∴AM⊥BC,…(3分)
∵底面ABC是边长为1的正三角形,
∴点M为BC中点.…(4分)
(2)解法一:过点B作BH⊥C1M,交其延长线于H,
由(1)知AM⊥C1M,AM⊥CB,
∴AM⊥平面C1CBB1,
∴AM⊥BH,∴BH⊥平面AMC1,
∴BH为点B到平面AMC1的距离,…(6分)
∴AM=C1M=
| ||
| 2 |
在Rt△CC1M中,解得CC1=
| ||
| 2 |
∵△BHM∽△C1CM,
∴
| BH |
| CC1 |
| BM |
| C1M |
| BH | ||||
|
| ||||
|
解得BH=
| ||
| 6 |
(2)解法二:设点B到平面AMC1的距离为h.
则VB-AMC1=VA-BMC1,…(5分)
由(I)知 AM⊥C1M,AM⊥CB,
∴AM⊥平面C1CBB1…(6分)
∵AB=1,BM=
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
∴
| 1 |
| 3 |
| 1 |
| 3 |
∴
| 1 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
解得h=
| ||
| 6 |
(3)解法一:过M作MH⊥AC于H,作MG⊥AC1于G,连结GH.

∵平面AC1⊥平面ABC,且面AC1∩面ABC=AC,
又MH?面ABC,MH⊥AC,∴MH⊥面AC1,∴MH⊥AC1,
又∵MG⊥AC1,且MH∩MG=M,
∴AC1⊥面MHG,∴AC1⊥GH,
故∠MGH为二面角M-AC1-C的平面角,…(11分)
由(1)知MH=
| 1 |
| 2 |
| ||
| 4 |
在等腰直角三角形AMC1中,MG=
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 4 |
∴sin∠MGH=
| MH |
| MG |
| ||
| 4 |
| 4 | ||
|
| ||
| 2 |
因为二面角M-AC1-C为锐二面角,故∠MGH=
| π |
| 4 |
所以二面角M-AC1-C的大小为
| π |
| 4 |
(3)解法二:过M作MM1∥CC1,交B1C1于M1.

以M为坐标原点,BC,AM,MM1分别为x轴,y轴,z轴,
建立空间直角坐标系.…(10分)
设面ACC1的一个法向量为
| μ |
则
|
| μ |
| 3 |
同理可求得面AMC1的一个法向量为
| v |
| 2 |
设二面角M-AC1-C的大小为θ,由图知θ为锐角,
故cosθ=|
| μ |
| v |
| ||
2
|
| ||
| 2 |
| π |
| 4 |
故二面角M-AC1-C的大小为
| π |
| 4 |
点评:本题考查点M为BC的中点的证明,考查点B到平面AMC1的距离的求法,考查二面角M-AC1-C的大小的求法,解题时要注意空间思维能力的培养.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
椭圆
+
=1的焦距是( )
| x2 |
| 9 |
| y2 |
| 5 |
| A、3 | ||
| B、6 | ||
C、2
| ||
| D、4 |
在极坐标系中,直线ρcosθ-ρsinθ-3=0与圆ρ=2cosθ的位置关系是( )
| A、相交但不过圆心 | B、相交且过圆心 |
| C、相离 | D、相切 |
已知函数f(x)=x2-5x+3-
,g(x)=-x+xlnx(k∈R),若对于?x1∈(1,+∞),?x2∈(0,+∞)都有f(x1)≥g(x2)成立,则k的取值范围( )
| k(x-1) |
| ex |
A、(-∞,
| ||
| B、(-∞,-e3] | ||
| C、(-∞,-e] | ||
D、(-∞,
|
曲线
+
=1与曲线
+
=1(12<k<16)的( )
| x2 |
| 16 |
| y2 |
| 12 |
| x2 |
| 16-x |
| y2 |
| 12-k |
| A、长轴长与实轴长相等 |
| B、短轴长与虚轴长相等 |
| C、焦距相等 |
| D、离心率相等 |