题目内容
若椭圆
+
=1(a>b>0)的离心率为
,则双曲线
-
=1的离心率为 .
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:利用椭圆
+
=1(a>b>0)的离心率为
,可得
=
,即a2=2b2,利用双曲线
-
=1的离心率
,即可得出结论.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| a2-b2 |
| a2 |
| 1 |
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
|
解答:
解:∵椭圆
+
=1(a>b>0)的离心率为
,
∴
=
,
∴a2=2b2,
∴双曲线
-
=1的离心率
=
,
故答案为:
.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
∴
| a2-b2 |
| a2 |
| 1 |
| 2 |
∴a2=2b2,
∴双曲线
| x2 |
| a2 |
| y2 |
| b2 |
|
| 3 |
故答案为:
| 3 |
点评:本题考查椭圆、双曲线的性质,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
函数f(x)=tx2+4tx+1(t>5),若x1>x2,x1+x2=1-t,则( )
| A、f(x1)>f(x2) |
| B、f(x1)<f(x2) |
| C、f(x1)=f(x2) |
| D、f(x1),f(x2)大小关系不能确定 |
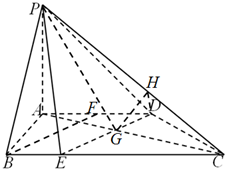 如图,在四棱锥PE=3中,AE=
如图,在四棱锥PE=3中,AE=