题目内容
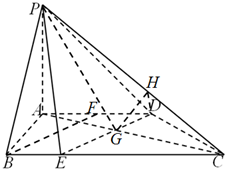如图，在四棱锥PE=3中，AE=| 5 |
| PE2-AE2 |
（Ⅰ）求证：平面∠GHD平面A-PC-D；
（Ⅱ）若直线PCA～与平面GCH所成的角的正弦值为
| PA |
| GH |
| PC |
| GC |
| CE2-EG2 |
6
| ||
| 5 |
考点：二面角的平面角及求法
专题：空间位置关系与距离,空间角
分析：（Ⅰ）首先利用线线的关系求出△BAF～△CBA，进一步知BF⊥AC，进一步求出线面垂直，即PA⊥平面ABCD
最后证出：ED⊥平面PAC，转化成平面PED⊥平面PAC．
（Ⅱ）先利用几何法作出二面角的平面角，然后利用相关的线段长求出△PCA～△GCH，
=
，而GC=
=
，GH=
=
最后求出tan∠GHD=
，再转化成余弦值，即得结果．
最后证出：ED⊥平面PAC，转化成平面PED⊥平面PAC．
（Ⅱ）先利用几何法作出二面角的平面角，然后利用相关的线段长求出△PCA～△GCH，
| PA |
| GH |
| PC |
| GC |
| CE2-EG2 |
6
| ||
| 5 |
| PA•GC |
| PC |
| ||
| 5 |
| ||
| 3 |
解答：
证明：（Ⅰ）取AD中点F，连接BF，则FD∥BE，FD=BE，
∴四边形FBED是平行四边形，∴FB∥ED
∵直角△BAF和直角△CBA中，
=
=2
∴△BAF～△CBA，
易知BF⊥AC
∴ED⊥AC
∵平面PAB⊥平面ABCD，平面PAB∩平面ABCD=AB
AB⊥PA
∴PA⊥平面ABCD
∴PA⊥ED，
∵PA∩AC=A
∴ED⊥平面PAC，
∴平面PED⊥平面PAC．
解：（Ⅱ）设ED交AC于G，连接PG，则∠EPG是直线PE与平面PAC所成的角．
设BE=1
由△AGD～△CGE，
知
=
=
，
∵AB=AD=2
∴EG=
DE=
，DG=
∵∴PE=3，AE=
，PA=
=2
作GH⊥PC于H，由PC⊥DE，知PC⊥平面HDG，
∴PC⊥DG，
∴∠GHD是二面角A-PC-D的平面角
∵△PCA～△GCH，
∴
=
，而GC=
=
∴GH=
=
∴tan∠GHD=
，
∴cos∠GHD=
，
即二面角A-PC-D的平面角的余弦值为
．
∴四边形FBED是平行四边形，∴FB∥ED
∵直角△BAF和直角△CBA中，
| BA |
| AF |
| CB |
| BA |
∴△BAF～△CBA，
易知BF⊥AC
∴ED⊥AC
∵平面PAB⊥平面ABCD，平面PAB∩平面ABCD=AB
AB⊥PA
∴PA⊥平面ABCD
∴PA⊥ED，
∵PA∩AC=A
∴ED⊥平面PAC，
∴平面PED⊥平面PAC．
解：（Ⅱ）设ED交AC于G，连接PG，则∠EPG是直线PE与平面PAC所成的角．
设BE=1
由△AGD～△CGE，
知
| DG |
| GE |
| AD |
| EC |
| 2 |
| 3 |
∵AB=AD=2
∴EG=
| 3 |
| 5 |
3
| ||
| 5 |
2
| ||
| 5 |
∵∴PE=3，AE=
| 5 |
| PE2-AE2 |
作GH⊥PC于H，由PC⊥DE，知PC⊥平面HDG，
∴PC⊥DG，
∴∠GHD是二面角A-PC-D的平面角
∵△PCA～△GCH，
∴
| PA |
| GH |
| PC |
| GC |
| CE2-EG2 |
6
| ||
| 5 |
∴GH=
| PA•GC |
| PC |
| ||
| 5 |
∴tan∠GHD=
| ||
| 3 |
∴cos∠GHD=
| ||
| 5 |
即二面角A-PC-D的平面角的余弦值为
| ||
| 5 |
点评：本题考查的知识要点：三角形的相似，线面垂直的判定定理，面面垂直的判定定理，二面角的平面角的做法及求值问题，属于中等题型．
练习册系列答案
考前必练系列答案
相关题目
已知3a=2，那么log38-2log36用a表示是（ ）
| A、a-2 |
| B、5a-2 |
| C、3a-（1+a）2 |
| D、3a-a2 |