题目内容
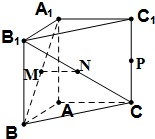 如图,在直三棱柱ABC-A1B1C1中,AB=1,AC=AA1=
如图,在直三棱柱ABC-A1B1C1中,AB=1,AC=AA1=| 3 |
(1)证明:MN⊥平面ABB1A1;
(2)若点P是CC1的中点,求四面体B1-APB的体积.
考点:直线与平面垂直的判定,棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:(1)由题可得AA1⊥A1C1且A1B1⊥A1C1,又因为AA1∩A1B1=A,所以A1C1⊥平面ABB1A1,继而得到MN⊥平面ABB1A1;
(2)由于VB1-APB=VP-ABB1,所以先求△ABB1的面积,由(1)知A1C1⊥平面ABB1A1,三棱锥的高是A1C1,所以根据三棱锥的体积公式可得体积.
(2)由于VB1-APB=VP-ABB1,所以先求△ABB1的面积,由(1)知A1C1⊥平面ABB1A1,三棱锥的高是A1C1,所以根据三棱锥的体积公式可得体积.
解答:
解:(1)证明:∵直三棱柱ABC-A1B1C1中,
AA1⊥底面A1B1C1,A1C1?平面A1B1C1,
∴AA1⊥A1C1.
∵直三棱柱ABC-A1B1C1中,
AB=1,AC=
,BC=2,
∴A1B1⊥A1C1,
又∵AA1∩A1B1=A,
∴A1C1⊥平面ABB1A1,
又∵点M是A1B的中点,点N是B1C的中点,
∴MN∥A1C1,
∴MN⊥平面ABB1A1;
(2)由(1)知,直三棱柱ABC-A1B1C1中,A1C1⊥平面ABB1A1,
∴三棱锥P-ABB1的高是A1C1,
∴三棱锥P-ABB1的体积为:
×S△ABB1×A1C1
=
×
×AB×AA1×A1C1=
×
×1×
×
=
又∵VB1-APB=VP-ABB1,
∴四面体B1-APB的体积为
.
AA1⊥底面A1B1C1,A1C1?平面A1B1C1,
∴AA1⊥A1C1.
∵直三棱柱ABC-A1B1C1中,
AB=1,AC=
| 3 |
∴A1B1⊥A1C1,
又∵AA1∩A1B1=A,
∴A1C1⊥平面ABB1A1,
又∵点M是A1B的中点,点N是B1C的中点,
∴MN∥A1C1,
∴MN⊥平面ABB1A1;
(2)由(1)知,直三棱柱ABC-A1B1C1中,A1C1⊥平面ABB1A1,
∴三棱锥P-ABB1的高是A1C1,
∴三棱锥P-ABB1的体积为:
| 1 |
| 3 |
=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
| 1 |
| 2 |
又∵VB1-APB=VP-ABB1,
∴四面体B1-APB的体积为
| 1 |
| 2 |
点评:证明线面垂直关键是证明已知直线与面内的两条相交直线都垂直即可,求三棱锥的体积时若不易求出一般是先观察一下是否换一个底面积与高都容易求的定点.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
从圆x2-2x+y2-2y+1=0外一点P(-1,1)向这个圆作两条切线,则该圆夹在两切线间的劣弧的长为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知sin(θ+π)=-
,且θ为第二象限角,则cos(θ-4π)=( )
| 3 |
| 5 |
A、
| ||
B、-
| ||
C、±
| ||
D、
|