题目内容
某几何体的三视图如图所示,则该几何体的体积为 .
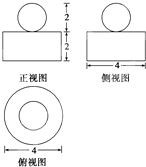

考点:由三视图求面积、体积
专题:空间位置关系与距离
分析:由已知中三视图可得该几何体为一个球与圆柱的组合体,分别求出球的体积和圆柱的体积,相加可得答案.
解答:
解:由已知中三视图可得该几何体为一个球与圆柱的组合体,
球的直径为2,故半径R=1,故球的体积为
π
圆柱的底面直径为4,故半径r=2,高为2,故圆柱的体积为8π
故该几何体的体积为
π+8π=
π
故答案为:
π
球的直径为2,故半径R=1,故球的体积为
| 4 |
| 3 |
圆柱的底面直径为4,故半径r=2,高为2,故圆柱的体积为8π
故该几何体的体积为
| 4 |
| 3 |
| 28 |
| 3 |
故答案为:
| 28 |
| 3 |
点评:本题考查的知识点是由三视图,求体积,其中根据已知分析出几何体的形状是解答的关键.

练习册系列答案
相关题目
直线l:(2-m)x+(m+1)y-3=0与圆C:(x-2)2+(y-3)2=9的交点个数为( )
| A、2 | B、1 | C、0 | D、与m有关 |
函数y=
的图象与y=3sinπx(-1≤x≤3)的图象所有交点横坐标之和为( )
| 1 |
| 1-x |
| A、2 | B、4 | C、6 | D、8 |
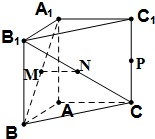 如图,在直三棱柱ABC-A1B1C1中,AB=1,
如图,在直三棱柱ABC-A1B1C1中,AB=1,