题目内容
选修4-5:不等式选讲
已知函数f(x)=|x+2|+|2x-4|
(1)求f(x)<6的解集;
(2)若关于x的不等式f(x)≥m2-3m的解集是R,求m的取值范围.
已知函数f(x)=|x+2|+|2x-4|
(1)求f(x)<6的解集;
(2)若关于x的不等式f(x)≥m2-3m的解集是R,求m的取值范围.
考点:绝对值不等式
专题:不等式的解法及应用
分析:(I)分当x≥2时、当2>x>-2时,当x≤-2时三种情况,分别去掉绝对值,求得不等式的解集,再取并集,即得所求.
(II)由函数f(x)的图象求得f(x)=|x+2|+|2x-4|的最小值为4,可得 m2-3m≤4,由此求得m的范围.
(II)由函数f(x)的图象求得f(x)=|x+2|+|2x-4|的最小值为4,可得 m2-3m≤4,由此求得m的范围.
解答:
解:(I)由题设知:当x≥2时,不等式等价与x+2+2x-4<6,即2≤x<
.
当2>x>-2时,不等式等价与x+2+4-2x<6,即2>x>0.
当x≤-2时,不等式等价于-x-2+4-2x<6,x无解.
综上可得,满足不等式的解是{x|0<x<
}.
(II)由函数f(x)的图象可得f(x)=|x+2|+|2x-4|的最小值为4,
则由题意可得 m2-3m≤4,解之得,-1≤m≤4.
| 8 |
| 3 |
当2>x>-2时,不等式等价与x+2+4-2x<6,即2>x>0.
当x≤-2时,不等式等价于-x-2+4-2x<6,x无解.
综上可得,满足不等式的解是{x|0<x<
| 8 |
| 3 |
(II)由函数f(x)的图象可得f(x)=|x+2|+|2x-4|的最小值为4,
则由题意可得 m2-3m≤4,解之得,-1≤m≤4.
点评:本题主要考查绝对值不等式的解法,绝对值不等式的性质,体现了转化、分类讨论的数学思想,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
一个几何体的三视图如图所示,其中俯视图是一个菱形,则该几何体的体积为( )


A、
| ||||
B、
| ||||
C、
| ||||
D、
|
某几何体的三视图如图所示,且该几何体的体积是2,则正(主)视图的面积等于( )


| A、2 | ||
B、
| ||
C、
| ||
| D、3 |
直线l:(2-m)x+(m+1)y-3=0与圆C:(x-2)2+(y-3)2=9的交点个数为( )
| A、2 | B、1 | C、0 | D、与m有关 |
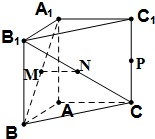 如图,在直三棱柱ABC-A1B1C1中,AB=1,
如图,在直三棱柱ABC-A1B1C1中,AB=1,