题目内容
已知sin(θ+π)=-
,且θ为第二象限角,则cos(θ-4π)=( )
| 3 |
| 5 |
A、
| ||
B、-
| ||
C、±
| ||
D、
|
考点:运用诱导公式化简求值
专题:计算题,三角函数的求值
分析:利用诱导公式求出sinθ,化简所求表达式,利用同角三角函数的基本关系式求解即可.
解答:
解:∵sin(θ+π)=-
,
∴sin(θ+π)=-sinθ=-
,
∴sinθ=
,θ为第二象限角,
cos(θ-4π)=cosθ=-
=-
=-
.
故选:B.
| 3 |
| 5 |
∴sin(θ+π)=-sinθ=-
| 3 |
| 5 |
∴sinθ=
| 3 |
| 5 |
cos(θ-4π)=cosθ=-
| 1-sin2θ |
1-(
|
| 4 |
| 5 |
故选:B.
点评:本题考查诱导公式求解三角函数值,同角三角函数的基本关系式的应用,考查计算能力.

练习册系列答案
相关题目
在直角坐标平面内,A点在(4,0),B点在圆(x-2)2+y2=1上,以AB为边作正△ABC(A、B、C按顺时针排列),则顶点C的轨迹是( )
| A、圆 | B、椭圆 |
| C、抛物线 | D、双曲线的一支 |
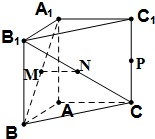 如图,在直三棱柱ABC-A1B1C1中,AB=1,
如图,在直三棱柱ABC-A1B1C1中,AB=1,