题目内容
已知二次函数f(x)=x2+2bx-1(b∈R).
(1)若函数y=f(x)与x轴的两个交A(x1,0),B(x2,0)点之间的距离为2,求b的值;
(2)若关于x的方程f(x)+x+b=0的两个实数根分别在区间(-3,-2),(0,1)内,求b的取值范围.
(1)若函数y=f(x)与x轴的两个交A(x1,0),B(x2,0)点之间的距离为2,求b的值;
(2)若关于x的方程f(x)+x+b=0的两个实数根分别在区间(-3,-2),(0,1)内,求b的取值范围.
考点:函数的零点与方程根的关系
专题:函数的性质及应用
分析:(1)根据二次函数根与系数之间的关系将条件|x1-x2|=2进行转化即可求b的值;
(2)根据方程和函数之间的关系,根据二次函数根的分布建立不等式关系即可得到结论.
(2)根据方程和函数之间的关系,根据二次函数根的分布建立不等式关系即可得到结论.
解答:
解:(1)∵函数y=f(x)与x轴的两个交A(x1,0),B(x2,0)点之间的距离为2,
∴|x1-x2|=2,
由f(x)=x2+2bx-1=0,
得x1+x2=-2b,x1x2=-1,
∵|x1-x2|2=|x1+x2|2-4x1x2=4,
∴4b2+4=4,即4b2=0,
解得b=0.
(2)∵f(x)+x+b=0,
∴设g(x)=x2+(2b+1)x+b-1,
∵方程f(x)+x+b=0的两个实数根分别在区间(-3,-2),(0,1)内,
∴满足
⇒
<b<1.
∴|x1-x2|=2,
由f(x)=x2+2bx-1=0,
得x1+x2=-2b,x1x2=-1,
∵|x1-x2|2=|x1+x2|2-4x1x2=4,
∴4b2+4=4,即4b2=0,
解得b=0.
(2)∵f(x)+x+b=0,
∴设g(x)=x2+(2b+1)x+b-1,
∵方程f(x)+x+b=0的两个实数根分别在区间(-3,-2),(0,1)内,
∴满足
|
| 1 |
| 3 |
点评:本题主要考查二次函数根的分布以及一元二次方程中根与系数之间的关系,考查学生的计算能力.

练习册系列答案
相关题目
| ∫ |
0 |
| A、0 | ||
| B、1 | ||
| C、2 | ||
D、
|
椭圆
(φ为参数)的长轴长为( )
|
| A、3 | B、5 | C、6 | D、10 |
直线l与圆x2+y2+2x-4y+1=0相交于A,B两点,若弦AB的中点(-2,3),则直线l的方程为( )
| A、x+y-3=0 |
| B、x+y-1=0 |
| C、x-y+5=0 |
| D、x-y-5=0 |
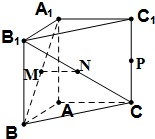 如图,在直三棱柱ABC-A1B1C1中,AB=1,
如图,在直三棱柱ABC-A1B1C1中,AB=1,