题目内容
若x+
≥4在x∈[3,4]内恒成立,则实数m的取值范围是 .
| m |
| x |
考点:基本不等式
专题:函数的性质及应用,不等式的解法及应用
分析:x+
≥4在x∈[3,4]内恒成立?m≥-x2+4x在x∈[3,4]内恒成立?m≥[-x2+4x]max,x∈[3,4].利用二次函数的单调性即可得出.
| m |
| x |
解答:
解:x+
≥4在x∈[3,4]内恒成立?m≥-x2+4x在x∈[3,4]内恒成立
?m≥[-x2+4x]max,x∈[3,4].
令f(x)=-x2+4x=-(x-2)2+4,x∈[3,4].
由二次函数的单调性可知:函数f(x)在区间[3,4]上单调递减.
∴f(x)max=f(3)=-(3-2)2+4=3.
∴实数m的取值范围是[3,+∞).
故答案为:[3,+∞).
| m |
| x |
?m≥[-x2+4x]max,x∈[3,4].
令f(x)=-x2+4x=-(x-2)2+4,x∈[3,4].
由二次函数的单调性可知:函数f(x)在区间[3,4]上单调递减.
∴f(x)max=f(3)=-(3-2)2+4=3.
∴实数m的取值范围是[3,+∞).
故答案为:[3,+∞).
点评:本题考查了恒成立问题的等价转化、二次函数的单调性,属于中档题.

练习册系列答案
相关题目
某几何体的三视图如图所示,且该几何体的体积是2,则正(主)视图的面积等于( )


| A、2 | ||
B、
| ||
C、
| ||
| D、3 |
直线l与圆x2+y2+2x-4y+1=0相交于A,B两点,若弦AB的中点(-2,3),则直线l的方程为( )
| A、x+y-3=0 |
| B、x+y-1=0 |
| C、x-y+5=0 |
| D、x-y-5=0 |
直线l:(2-m)x+(m+1)y-3=0与圆C:(x-2)2+(y-3)2=9的交点个数为( )
| A、2 | B、1 | C、0 | D、与m有关 |
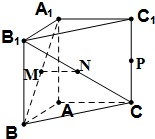 如图,在直三棱柱ABC-A1B1C1中,AB=1,
如图,在直三棱柱ABC-A1B1C1中,AB=1,