题目内容
已知函数f(x)=log2x,若数列{an}的各项使得2,f(a1),f(a2),f(a3),…,f(an),2n+4成等差数列,则数列{an}的前n项和Sn= .
考点:数列的求和
专题:等差数列与等比数列
分析:利用等差数列的通项公式可得公差d,再利用通项公式及其对数的运算性质、等差数列的前n项和公式即可得出.
解答:
解:∵2,f(a1),f(a2),f(a3),…,f(an),2n+4成等差数列,设公差为d.
∴2n+4=2+(n+2-1)d,解得d=2.
∴f(an)=2+(n+1-1)×2=2n+2,
∵函数f(x)=log2x,
∴log2an=2n+2,
解得an=22n+2=4n+1.
∴数列{an}的前n项和Sn=
=
(4n-1).
故答案为:
(4n-1).
∴2n+4=2+(n+2-1)d,解得d=2.
∴f(an)=2+(n+1-1)×2=2n+2,
∵函数f(x)=log2x,
∴log2an=2n+2,
解得an=22n+2=4n+1.
∴数列{an}的前n项和Sn=
| 8(4n-1) |
| 4-1 |
| 8 |
| 3 |
故答案为:
| 8 |
| 3 |
点评:本题考查了等差数列的通项公式及其对数的运算性质、等差数列的前n项和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
已知函数f(x)是定义在R上的奇函数,其导函数为f′(x),当x<0时,2f(x)+xf′(x)<0恒成立,则f(1),2014f(
),2015f(
)在大小关系为( )
| 2014 |
| 2015 |
A、2015f(
| ||||
B、2015f(
| ||||
C、f(1)<2015f(
| ||||
D、f(1)<2014f(
|
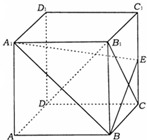 长方体ABCD-A1B1C1D1中,AA1=2,BC=
长方体ABCD-A1B1C1D1中,AA1=2,BC= 如图,在?ABCD中,E是AD上的一点,且AE=AB,BE和CD的延长线交于点F,且∠BFC=35°,求?ABCD的各内角的度数.
如图,在?ABCD中,E是AD上的一点,且AE=AB,BE和CD的延长线交于点F,且∠BFC=35°,求?ABCD的各内角的度数.