题目内容
已知函数f（x）是定义在R上的奇函数，其导函数为f′（x），当x＜0时，2f（x）+xf′（x）＜0恒成立，则f（1），2014f(
)，2015f(
)在大小关系为（ ）
| 2014 |
| 2015 |
A、2015f(
| ||||
B、2015f(
| ||||
C、f（1）＜2015f(
| ||||
D、f（1）＜2014f(
|
考点：利用导数研究函数的单调性,函数奇偶性的性质,导数的运算
专题：函数的性质及应用,导数的概念及应用
分析：首先利用换元法设g（x）=x2f（x），进一步利用函数的导数求出函数g（x）的单调性，再利用函数的奇偶性求出函数在对称区间里的单调性，最后求出函数大小关系．
解答：
解：已知函数f（x）是定义在R上的奇函数，其导函数为f′（x），
则：设函数g（x）=x2f（x）
则：g′（x）=2xf（x）+x2f′（x）
=g′（x）=x（2f（x）+xf′（x））
当x＜0时，2f（x）+xf′（x）＜0恒成立，
则：函数g′（x）＞0
所以函数在x＜0时，函数g（x）为单调递增函数．
由于函数f（x）是定义在R上的奇函数，
则：函数g（x）=x2f（x）为奇函数．
所以：在x＞0时，函数g（x）为单调递增函数．
所以：g（
）＞g(
)＞g(1)
即：2015f(
)＞2014f(
)＞f(1)
故选：D
则：设函数g（x）=x2f（x）
则：g′（x）=2xf（x）+x2f′（x）
=g′（x）=x（2f（x）+xf′（x））
当x＜0时，2f（x）+xf′（x）＜0恒成立，
则：函数g′（x）＞0
所以函数在x＜0时，函数g（x）为单调递增函数．
由于函数f（x）是定义在R上的奇函数，
则：函数g（x）=x2f（x）为奇函数．
所以：在x＞0时，函数g（x）为单调递增函数．
所以：g（
| 2015 |
| 2014 |
即：2015f(
| 2015 |
| 2014 |
故选：D
点评：本题考查的知识要点：利用函数的导数求函数的单调性，函数的奇偶性和函数单调性的关系．
练习册系列答案
相关题目
在△ABC中，AB=4，AC=3，∠A=60°，点H是△ABC的垂心，设存在实数λ，μ，使
=λ
+μ
，则（ ）
| AH |
| AB |
| AC |
A、λ=
| ||||
B、λ=
| ||||
C、λ=
| ||||
D、λ=
|
用数学归纳法证明：1+
+
+…+
＜k+1（n∈N*），由n=k（k∈N*）不等式成立，推证n=k+1时，左边应增加的项数是（ ）
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2n |
| A、2k |
| B、2k-1 |
| C、2k+1 |
| D、2k-1 |
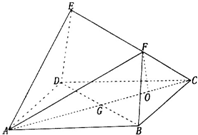如图正方形ABCD的边长为ABCD的边长为2