题目内容
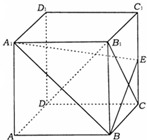 长方体ABCD-A1B1C1D1中,AA1=2,BC=
长方体ABCD-A1B1C1D1中,AA1=2,BC=| 2 |
(Ⅰ)求证:平面A1BE⊥平面B1CD;
(Ⅱ)平面A1BE与底面A1B1C1D1所成的锐二面角的大小为θ,当
2
| ||
| 5 |
| 2 |
考点:用空间向量求平面间的夹角,平面与平面垂直的判定
专题:综合题,空间位置关系与距离,空间角
分析:(Ⅰ)证明:平面A1BE⊥平面B1CD,只需要证明BE⊥平面B1CD即可;
(Ⅱ)以D为坐标原点,建立坐标系,设AB=a,求出平面A1BE的法向量,底面A1B1C1D1的法向量,利用向量的夹角公式,结合
<AB<2
,即可求θ的取值范围.
(Ⅱ)以D为坐标原点,建立坐标系,设AB=a,求出平面A1BE的法向量,底面A1B1C1D1的法向量,利用向量的夹角公式,结合
2
| ||
| 5 |
| 2 |
解答:
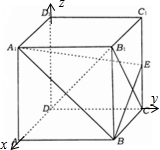 (Ⅰ)证明:∵CD⊥平面BCC1B1,
(Ⅰ)证明:∵CD⊥平面BCC1B1,
∴CD⊥BE,
∵E为CC1的中点,
∴△B1BC∽△BCE,
∴∠EBC=∠BB1C,
∴∠EBB1+∠BB1C=90°,
∴BE⊥B1C,
∴B1C∩CD=C,
∴BE⊥平面B1CD,
∵BE?平面A1BE,
∴平面A1BE⊥平面B1CD;
(Ⅱ)解:以D为坐标原点,建立坐标系,设AB=a,则
A1(
,0,2),B(
,a,0),E(0,a,1),
∴
=(0,a,-2),
=(-
,a,-1),
设平面A1BE的法向量为
=(x,y,z),则
,
∴可取
=(
,1,
)
∵底面A1B1C1D1的法向量为
=(0,0,1),
∴cosθ=
=
,
∵
<AB<2
,
∴
<a2<8,
∴
<
<2,
∴
<cosθ<
,
∴
<θ<
.
 (Ⅰ)证明:∵CD⊥平面BCC1B1,
(Ⅰ)证明:∵CD⊥平面BCC1B1,∴CD⊥BE,
∵E为CC1的中点,
∴△B1BC∽△BCE,
∴∠EBC=∠BB1C,
∴∠EBB1+∠BB1C=90°,
∴BE⊥B1C,
∴B1C∩CD=C,
∴BE⊥平面B1CD,
∵BE?平面A1BE,
∴平面A1BE⊥平面B1CD;
(Ⅱ)解:以D为坐标原点,建立坐标系,设AB=a,则
A1(
| 2 |
| 2 |
∴
| A1B |
| A1E |
| 2 |
设平面A1BE的法向量为
| n |
|
∴可取
| n |
| a | ||
2
|
| a |
| 2 |
∵底面A1B1C1D1的法向量为
| m |
∴cosθ=
|
| ||||
|
| 1 | ||||||
|
∵
2
| ||
| 5 |
| 2 |
∴
| 8 |
| 5 |
∴
| 2 |
|
∴
| 1 |
| 2 |
| 1 | ||
|
∴
| π |
| 4 |
| π |
| 3 |
点评:本题考查线面、面面垂直,考查空间角,考查向量知识的运用,知识综合性强.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
一个几何体的三视图如图所示,则这个几何体的体积是( )
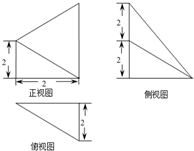

| A、1 | B、2 | C、3 | D、4 |
如图所示是一个几何体的三视图,则该几何体的体积为( )


| A、8+2π | B、16+2π |
| C、8+π | D、16+π |
已知函数f(x)=
,则下列关于函数y=f[f(kx)+1]+1(k≠0)的零点个数的判断正确的是( )
|
| A、当k>0时,有3个零点;当k<0时,有4个零点 |
| B、当k>0时,有4个零点;当k<0时,有3个零点 |
| C、无论k为何值,均有3个零点 |
| D、无论k为何值,均有4个零点 |
