题目内容
已知
≤1-
x+
x2,x∈[0,+∞),证明不等式恒不成立.
| 1 | ||
|
| 1 |
| 2 |
| 1 |
| 4 |
考点:函数恒成立问题
专题:函数的性质及应用,不等式的解法及应用
分析:求出当x∈[0,+∞)时,1-
x+
x2的最小值
,
的最大值1,取x=
,计算即可判断不等式恒不成立.
| 1 |
| 2 |
| 1 |
| 4 |
| 3 |
| 4 |
| 1 | ||
|
| 1 |
| 2 |
解答:
证明:当x∈[0,+∞)时,
1-
x+
x2=
(x2-2x+4)=
[(x-1)2+3],
当x=1时,取得最小值
.此时
=
,有
<
;
当x=0时,取得最大值1,此时1-
x+
x2=1,有1≤1;
当x=
时,
=
,1-
x+
x2=
,即有
>
.
则有不等式在x∈[0,+∞]恒不成立.
1-
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
当x=1时,取得最小值
| 3 |
| 4 |
| 1 | ||
|
| ||
| 2 |
| ||
| 2 |
| 3 |
| 4 |
| 1 | ||
|
| 1 |
| 2 |
| 1 |
| 4 |
当x=
| 1 |
| 2 |
| 1 | ||
|
| ||
| 3 |
| 1 |
| 2 |
| 1 |
| 4 |
| 13 |
| 16 |
| ||
| 3 |
| 13 |
| 16 |
则有不等式在x∈[0,+∞]恒不成立.
点评:本题考查不等式恒不成立问题,主要考查转化思想,求出函数的最值是解题的关键.

练习册系列答案
相关题目
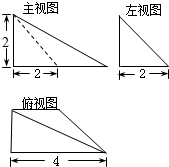 已知一个空间几何体的三视图如图所示,根据图中标出的尺寸,可得这个几何体的体积是( )
已知一个空间几何体的三视图如图所示,根据图中标出的尺寸,可得这个几何体的体积是( )| A、2 | B、4 | C、6 | D、12 |
在△ABC中,AB=4,AC=3,∠A=60°,点H是△ABC的垂心,设存在实数λ,μ,使
=λ
+μ
,则( )
| AH |
| AB |
| AC |
A、λ=
| ||||
B、λ=
| ||||
C、λ=
| ||||
D、λ=
|
