题目内容
已知a=21.5,b=log21.5,c=log1.51.2,则( )
| A、a<b<c |
| B、c<b<a |
| C、c<a<b |
| D、b<c<a |
考点:对数值大小的比较
专题:函数的性质及应用
分析:由于1>b=log21.5>log2
=
,c=log1.51.2<log1.5
=
,可得c<b.再利用指数函数的单调性可得a>1即可.
| 2 |
| 1 |
| 2 |
| 1.5 |
| 1 |
| 2 |
解答:
解:∵a=21.5>1,1>b=log21.5>log2
=
,c=log1.51.2<log1.5
=
,
∴c<b<a.
故选:B.
| 2 |
| 1 |
| 2 |
| 1.5 |
| 1 |
| 2 |
∴c<b<a.
故选:B.
点评:本题考查了指数与对数函数的单调性,属于基础题.

练习册系列答案
相关题目
设M=
,N=
,P=
,Q
,则M与N、P与Q的大小关系为( )
| 102012+1 |
| 102013+1 |
| 102013+1 |
| 102014+1 |
| 102012+9 |
| 102013+100 |
| 102013+9 |
| 102014+100 |
| A、M>N,P<Q |
| B、M>N,P<Q |
| C、M>N,P<Q |
| D、M>N,P<Q |
下列说法错误的是( )
| A、在统计里,把所需考察对象的全体叫作总体 |
| B、平均数、众数与中位数从不同的角度描述了一组数据的集中趋势 |
| C、一组数据的平均数一定大于这组数据中的每个数据 |
| D、一组数据的方差越大,说明这组数据的波动越大 |
下列函数中,既是偶函数,又是在区间(0,+∞)上单调递减的函数是( )
A、y=ln
| ||
| B、y=x3 | ||
| C、y=2|x| | ||
D、y=x
|
已知定义在R上的函数f(x)满足f[f(x)]=xf(x)+1,则方程f(x)=0的实根个数为( )
| A、0 | B、1 | C、2 | D、4 |
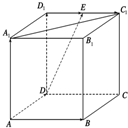 如图所示,在正方体ABCD-A1B1C1D1中,E为D1C1的中点,N为BC的中点.
如图所示,在正方体ABCD-A1B1C1D1中,E为D1C1的中点,N为BC的中点.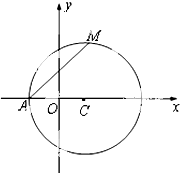 如图,已知圆C:(x-1)2+y2=r2(r>1),设A为圆C与x轴负半轴的交点,过点A作圆C的弦AM,并使弦AM的中点恰好落在y轴上.
如图,已知圆C:(x-1)2+y2=r2(r>1),设A为圆C与x轴负半轴的交点,过点A作圆C的弦AM,并使弦AM的中点恰好落在y轴上.