Question

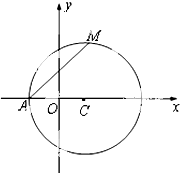如图，已知圆C：（x-1）²+y²=r²（r＞1），设A为圆C与x轴负半轴的交点，过点A作圆C的弦AM，并使弦AM的中点恰好落在y轴上．
（1）当r在（1，+∞）内变化时，求点M的轨迹E的方程；
（2）已知定点P（-1，1）和Q（1，0），设直线PM、QM与轨迹E的另一个交点分别是M₁、M₂．求证：当M点在轨迹E上变动时，只要M₁、M₂都存在且M₁≠M₂，则直线M₁M₂恒过一个定点，并求出这个定点．

Answer 1

考点：圆锥曲线的轨迹问题

专题：综合题,圆锥曲线的定义、性质与方程

分析：（1）设M（x，y），则AM的中点D(0，

y

2

)．利用CD⊥DM，建立方程，由此能求出点M的轨迹E的方程．
（2）设M，M₁，M₂的坐标分别为(t2，2t)，(

t

2 1

，2t1)，(

t

2 2

，2t2)，其中t≠0且t≠

1

2

．由P，M，M₁共线得

2t1-2t

t 2 1 -t2

=

2t-1

t2+1

⇒t1=

t+2

2t-1

； 由Q，M，M₂共线得

2t2-2t

t 2 2 -t2

=

2t-0

t2-1

⇒t2=-

1

t

，可得t₁t₂=-

t+2

2t2-t

，t₁+t₂=

t2+1

2t2-t

，求出直线M₁M₂的方程，即可得出结论．

解答： 解：（1）设M（x，y），则AM的中点D(0，

y

2

)．
因为C（1，0），

DC

=（1，-

y

2

），

DM

=（x，

y

2

）
在⊙C中，因为CD⊥DM，所以x-

y2

4

=0．
所以，点M的轨迹E的方程为：y²=4x（x≠0）．
（2）设M，M₁，M₂的坐标分别为(t2，2t)，(

t

2 1

，2t1)，(

t

2 2

，2t2)，其中t≠0且t≠

1

2

．
由P，M，M₁共线得

2t1-2t

t 2 1 -t2

=

2t-1

t2+1

⇒t1=

t+2

2t-1

；
由Q，M，M₂共线得

2t2-2t

t 2 2 -t2

=

2t-0

t2-1

⇒t2=-

1

t

．
∴t₁t₂=-

t+2

2t2-t

，t₁+t₂=

t2+1

2t2-t

∴直线M₁M₂的方程为（t₁+t₂）y-2x-2t₁t₂=0，即t²（y-4x）+2t（x+1）+（y+4）=0，
∴

y-4x=0 x+1=0 y+4=0

，
∴x=-1，y=-4，
∴直线M₁M₂恒过一个定点（-1，-4）．

点评：本题考查轨迹方程，考查直线过定点，考查学生分析解决问题的能力，属于中档题．