题目内容
在△ABC中，A、B、C的对边为a、b、c，且2sinAsinC=sinAsinB+sinBsinC．
（Ⅰ）求角B的最大值；
（Ⅱ）设向量
=（
cos
+sin
，-1），
=（2cos
，
），求
•
的取值范围．
（Ⅰ）求角B的最大值；
（Ⅱ）设向量
| a |
| 3 |
| B |
| 2 |
| B |
| 2 |
| b |
| B |
| 2 |
| 3 |
| a |
| b |
考点：平面向量数量积的运算,正弦定理,余弦定理
专题：解三角形,平面向量及应用
分析：（I）由2sinAsinC=sinAsinB+sinBsinC，利用正弦定理可得2ac=ab+bc，由余弦定理可得cosB=
=
+
-
，再利用基本不等式可得cosB≥1-
=
，利用y=cosx在（0，π）上单调递减，可得B的取值范围．
（II）
•
=
•2cos2
+sinB-
=
cosB+sinB=2sin(B+
)，利用B∈(0，
]，可得(B+
)∈(
，
]，即可得出
•
的取值范围．
| a2+c2-b2 |
| 2ac |
| c |
| 2a |
| a |
| 2c |
| 1 | ||||
|
| 1 |
| 2 |
| 1 |
| 2 |
（II）
| a |
| b |
| 3 |
| B |
| 2 |
| 3 |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
| a |
| b |
解答：
解：（I）∵2sinAsinC=sinAsinB+sinBsinC，利用正弦定理可得2ac=ab+bc，∴b=
．
由余弦定理可得cosB=
=
=
+
-
，∵
+
≥2
=1，当且仅当a=c时取等号．
∴cosB≥1-
=
，
又∵y=cosx在（0，π）上单调递减，∴B的取值范围是(0，
]．因此角B的最大值是
．
（II）
•
=
•2cos2
+sinB-
=
cosB+sinB=2sin(B+
)，
∵B∈(0，
]，∴(B+
)∈(
，
]，
∴
≤2sin(B+
)≤2，∴
•
的取值范围是[
，2]．
| 2ac |
| a+c |
由余弦定理可得cosB=
| a2+c2-b2 |
| 2ac |
a2+c2-(
| ||
| 2ac |
| c |
| 2a |
| a |
| 2c |
| 1 | ||||
|
| c |
| 2a |
| a |
| 2c |
|
∴cosB≥1-
| 1 |
| 2 |
| 1 |
| 2 |
又∵y=cosx在（0，π）上单调递减，∴B的取值范围是(0，
| π |
| 3 |
| π |
| 3 |
（II）
| a |
| b |
| 3 |
| B |
| 2 |
| 3 |
| 3 |
| π |
| 3 |
∵B∈(0，
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
∴
| 3 |
| π |
| 3 |
| a |
| b |
| 3 |
点评：本题综合考查了数量积运算、正弦定理和余弦定理、基本不等式的性质、倍角公式、三角函数的单调性等基础知识与基本技能方法，考查了推理能力和计算能力，属于难题．
练习册系列答案
相关题目
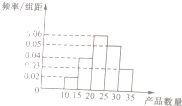为了调查某厂数万名工人独立生产某种产品的能力，随机抽查了m位工人某天独立生产该产品的数量，产品数量的分组区间为[10，15），[15，20），[20，25），[25，30），[30，35），频率分布直方图如图所示，已知独立生产的产品数量在[20，25）之间的工人有6位．
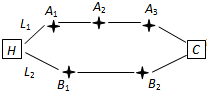家住H小区的王先生开车到C单位上班有L1、L2两条路线（如图），其中路线L1上有A1、A2、A3三个路口，各路口遇到红灯的概率均为
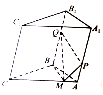如图，在三棱柱ABC-A1B1C1的侧棱A1A和B1B上各有一个动点P，Q，且满足A1P=BQ，M是棱CA上的动点，则