Question

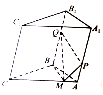如图，在三棱柱ABC-A₁B₁C₁的侧棱A₁A和B₁B上各有一个动点P，Q，且满足A₁P=BQ，M是棱CA上的动点，则

VM-ABQP

VABC-A1B1C1-VM-ABQP

的最大值是

 

．

Answer 1

考点：棱柱、棱锥、棱台的体积

专题：综合题,空间位置关系与距离

分析：由已知中A₁P=BQ，我们可得四边形PQBA与四边形PQB₁A₁的面积相等，等于侧面ABPQB₁A₁的面积的一半，M是棱CA上的动点，可得M是C时，

VM-ABQP

VABC-A1B1C1-VM-ABQP

最大．根据等底同高的棱锥体积相等，可将四棱椎C-PQBA的体积转化三棱锥C-ABA₁的体积，进而根据同底同高的棱锥体积为棱柱的

1

3

，求出四棱椎C-PQBA的体积，进而得到答案．

解答： 解：设三棱柱ABC-A₁B₁C₁的体积为V
∵侧棱AA₁和BB₁上各有一动点P，Q满足A₁P=BQ，
∴四边形PQBA与四边形PQB₁A₁的面积相等，
∵M是棱CA上的动点，
∴M是C时，

VM-ABQP

VABC-A1B1C1-VM-ABQP

最大
又四棱椎M-PQBA的体积等于三棱锥C-ABA₁的体积等于

1

3

V，
∴

VM-ABQP

VABC-A1B1C1-VM-ABQP

的最大值是

1 3 V

V- 1 3 V

=

1

2

．
故答案为：

1

2

．

点评：本题考查的知识点是棱柱的体积，棱锥的体积，其中根据四边形PQBA与四边形PQB₁A₁的面积相等，等于侧面ABPQB₁A₁的面积的一半，将四棱椎C-PQBA的体积转化三棱锥C-ABA₁的体积是解答本题的关键．