题目内容
| 1 |
| 2 |
| ||
| 2 |
| A、sin(α+30°) |
| B、sin(α-30°) |
| C、cos(α+30°) |
| D、cos(α-30°) |
考点:两角和与差的正弦函数
专题:三角函数的求值
分析:利用特殊角的三角函数值与两角差的余弦即可得到答案.
解答:
解:
sinα+
cosα
=sin
sinα+cos
cosα
=cos(α-
)
=cos(α-30°),
故选:D.
| 1 |
| 2 |
| ||
| 2 |
=sin
| π |
| 6 |
| π |
| 6 |
=cos(α-
| π |
| 6 |
=cos(α-30°),
故选:D.
点评:本题考查两角差的余弦公式的应用,属于基础题.

练习册系列答案
相关题目
已知直线x=2及x=4与函数y=log2x图象的交点分别为A,B,与函数y=lgx图象的交点分别为C,D,则直线AB与CD( )
| A、平行 | B、垂直 | C、不确定 | D、相交 |
 运行如图所示的程序框图,输出A,B,C的一组数据为
运行如图所示的程序框图,输出A,B,C的一组数据为 | 3 |
| A、垂直、相切 |
| B、平行、相交 |
| C、垂直、相离 |
| D、平行、相切 |
下列关于正弦定理的叙述或变形中错误的是( )
| A、在△ABC中,a:b:c=sinA:sinB:sinC | ||||
| B、在△ABC中,a=b?sin2A=sin2B | ||||
C、△ABC中:
| ||||
| D、△ABC中,正弦值较大的角所对的边也较大 |
已知
=(2,-2
),
=(-7,0),则
与
的夹角为( )
| a |
| 3 |
| b |
| a |
| b |
| A、30° | B、60° |
| C、120° | D、150° |
如图所示,不等式x(y-x-1)>0 表示的平面区域是( )
A、 |
B、 |
C、 |
D、 |
已知Rt△ABC中,∠C=90°,AB=5,BC=4,以BC为直径的圆交AB于D,则BD的长为( )
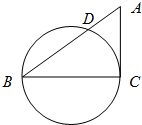

| A、4 | ||
B、
| ||
C、
| ||
D、
|
 用4种不同的颜色给图中A、B、C、D四个区域涂色,要求相邻的区域涂色不同,则不同的涂色方法共有
用4种不同的颜色给图中A、B、C、D四个区域涂色,要求相邻的区域涂色不同,则不同的涂色方法共有