题目内容
已知抛物线C:x2=2py(p>0),定点M(0,5),直线l:y=
与y轴交于点F,O为原点,若以OM为直径的圆恰好过l与抛物线C的交点.则抛物线C的方程为 .
| p |
| 2 |
考点:抛物线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:利用定点M(0,5),直线l:y=
与y轴交于点F,O为原点,以OM为直径的圆恰好过l与抛物线C的交点,建立方程,求出p,即可求抛物线C的方程
| p |
| 2 |
解答:
解:∵定点M(0,5),直线l:y=
与y轴交于点F,O为原点,以OM为直径的圆恰好过l与抛物线C的交点,
∴p2=
(5-
),
∴p=2,
∴抛物线C的方程为x2=4y.
故答案为:x2=4y.
| p |
| 2 |
∴p2=
| p |
| 2 |
| p |
| 2 |
∴p=2,
∴抛物线C的方程为x2=4y.
故答案为:x2=4y.
点评:本题考查抛物线的方程,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
| 1 |
| 2 |
| ||
| 2 |
| A、sin(α+30°) |
| B、sin(α-30°) |
| C、cos(α+30°) |
| D、cos(α-30°) |
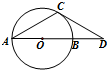 如图,已知点D在圆O直径AB的延长线上,过D作圆O的切线,切点为C.若CD=
如图,已知点D在圆O直径AB的延长线上,过D作圆O的切线,切点为C.若CD=