题目内容
如图所示,不等式x(y-x-1)>0 表示的平面区域是( )
A、 |
B、 |
C、 |
D、 |
考点:二元一次不等式(组)与平面区域
专题:不等式的解法及应用
分析:可化为
或
,结合选项可得.
|
|
解答:
解:不等式x(y-x-1)>0 可化为
或
,
由不等式组和平面区域的关系可知选项B正确.
故选:B
|
|
由不等式组和平面区域的关系可知选项B正确.
故选:B
点评:本题考查不等式与平面区域,转化为不等式组是解决问题的关键,属基础题.

练习册系列答案
相关题目
| 1 |
| 2 |
| ||
| 2 |
| A、sin(α+30°) |
| B、sin(α-30°) |
| C、cos(α+30°) |
| D、cos(α-30°) |
若复数z满足
=2i,则z的虚部为( )
| z |
| 1+i |
| A、-2 | B、-2i | C、2 | D、2i |
设x0是方程lnx+x-5=0的根,则x0在下列哪个区间内( )
| A、(1,2) |
| B、(2,3) |
| C、(3,4) |
| D、(4,5) |
已知a=cos2
-sin2
,b=sin1,c=
,则a,b,c的大小关系是( )
| π |
| 6 |
| π |
| 6 |
| tan30° |
| 1-tan230° |
| A、a<b<c |
| B、a>b>c |
| C、c>a>b |
| D、a<c<b |
函数f(x)=x2+3x-4的零点个数是( )
| A、1 | B、2 | C、3 | D、以上都不对 |
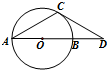 如图,已知点D在圆O直径AB的延长线上,过D作圆O的切线,切点为C.若CD=
如图,已知点D在圆O直径AB的延长线上,过D作圆O的切线,切点为C.若CD=