题目内容
已知直线x=2及x=4与函数y=log2x图象的交点分别为A,B,与函数y=lgx图象的交点分别为C,D,则直线AB与CD( )
| A、平行 | B、垂直 | C、不确定 | D、相交 |
考点:对数函数的图像与性质,指数函数的图像与性质
专题:函数的性质及应用
分析:先求出四个交点的坐标,进而分别求出直线AB,CD的解析式得出答案.
解答:
解:当x=2时,y=log22=1,x=4时,y=log24=2
∴A坐标为(2,1),B坐标为(4,2)
设直线AB解析式为y=kx+b,则有
,
解得k=
,b=0,
∴直线AB的解析式为y=
x,
同理可求出直线CD的解析式为y=
xlg2,
两条直线斜率不等,且乘积不为-1,
故直线AB,CD不平行,不垂直,
即直线AB,CD相交,
故选:D
∴A坐标为(2,1),B坐标为(4,2)
设直线AB解析式为y=kx+b,则有
|
解得k=
| 1 |
| 2 |
∴直线AB的解析式为y=
| 1 |
| 2 |
同理可求出直线CD的解析式为y=
| 1 |
| 2 |
两条直线斜率不等,且乘积不为-1,
故直线AB,CD不平行,不垂直,
即直线AB,CD相交,
故选:D
点评:本题主要考查了函数的图象.解此类题可以用数形结合的方式解决.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设f′(x0)=2,下面说法不正确的是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
| 1 |
| 2 |
| ||
| 2 |
| A、sin(α+30°) |
| B、sin(α-30°) |
| C、cos(α+30°) |
| D、cos(α-30°) |
函数f(x)=x2+3x-4的零点个数是( )
| A、1 | B、2 | C、3 | D、以上都不对 |
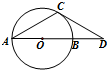 如图,已知点D在圆O直径AB的延长线上,过D作圆O的切线,切点为C.若CD=
如图,已知点D在圆O直径AB的延长线上,过D作圆O的切线,切点为C.若CD=