题目内容
 用4种不同的颜色给图中A、B、C、D四个区域涂色,要求相邻的区域涂色不同,则不同的涂色方法共有
用4种不同的颜色给图中A、B、C、D四个区域涂色,要求相邻的区域涂色不同,则不同的涂色方法共有考点:排列、组合及简单计数问题
专题:计算题,排列组合
分析:先涂A有C41=4种涂法,则涂B有C31=3种涂法,C与A,B相邻,则C有C21=2种涂法,D只与C相邻,则D有C31=3种涂法,根据分步计数原理,可得结论.
解答:
解:根据题意本题是一个分步计数问题,
首先涂A有C41=4种涂法,则涂B有C31=3种涂法,
C与A,B相邻,则C有C21=2种涂法,
D只与C相邻,则D有C31=3种涂法.
所以根据分步计数原理知共有4×3×2×3=72种涂法,
故答案为:72.
首先涂A有C41=4种涂法,则涂B有C31=3种涂法,
C与A,B相邻,则C有C21=2种涂法,
D只与C相邻,则D有C31=3种涂法.
所以根据分步计数原理知共有4×3×2×3=72种涂法,
故答案为:72.
点评:本题考查计数原理的应用,本题解题的关键是分析题目时时要按一定顺序,由相邻情况来确定可以涂色的情况数目,最后根据分步计数原理得到结果.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
| 1 |
| 2 |
| ||
| 2 |
| A、sin(α+30°) |
| B、sin(α-30°) |
| C、cos(α+30°) |
| D、cos(α-30°) |
已知a=cos2
-sin2
,b=sin1,c=
,则a,b,c的大小关系是( )
| π |
| 6 |
| π |
| 6 |
| tan30° |
| 1-tan230° |
| A、a<b<c |
| B、a>b>c |
| C、c>a>b |
| D、a<c<b |
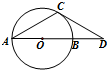 如图,已知点D在圆O直径AB的延长线上,过D作圆O的切线,切点为C.若CD=
如图,已知点D在圆O直径AB的延长线上,过D作圆O的切线,切点为C.若CD=