题目内容
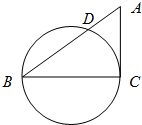
已知Rt△ABC中，∠C=90°，AB=5，BC=4，以BC为直径的圆交AB于D，则BD的长为（ ）
| A、4 | ||
B、
| ||
C、
| ||
D、
|
考点：弦切角
专题：直线与圆
分析：由勾股定理求出AC=3，由题意知AC是圆的切线，由此利用切割线定理能求出BD的长．
解答：
解：Rt△ABC中，
∵∠C=90°，AB=5，BC=4，
∴AC=
=3，
∵以BC为直径的圆交AB于D，
∴AC是圆的切线，
∴AC2=AD•AB，
∴AD=
=
，
∴BD=5-
=
．
故选：D．
∵∠C=90°，AB=5，BC=4，
∴AC=
| 25-16 |
∵以BC为直径的圆交AB于D，
∴AC是圆的切线，
∴AC2=AD•AB，
∴AD=
| AC2 |
| AB |
| 9 |
| 5 |
∴BD=5-
| 9 |
| 5 |
| 16 |
| 5 |
故选：D．
点评：本题考查线段长的求法，是基础题，解题时要认真审题，注意切割线定理的合理运用．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
| 1 |
| 2 |
| ||
| 2 |
| A、sin（α+30°） |
| B、sin（α-30°） |
| C、cos（α+30°） |
| D、cos（α-30°） |
已知a=cos2
-sin2
，b=sin1，c=
，则a，b，c的大小关系是（ ）
| π |
| 6 |
| π |
| 6 |
| tan30° |
| 1-tan230° |
| A、a＜b＜c |
| B、a＞b＞c |
| C、c＞a＞b |
| D、a＜c＜b |
函数f（x）=x2+3x-4的零点个数是（ ）
| A、1 | B、2 | C、3 | D、以上都不对 |
如图是一个几何体的三视图，根据图中数据，可得该几何体的体积是（ ）
A、π+
| ||
B、π+2
| ||
C、2π+
| ||
D、2π+2
|
函数y=-cos（
-
）的单调递增区间是（ ）
| π |
| 3 |
| x |
| 2 |
A、[2kπ-
| ||||
B、[4kπ-
| ||||
C、[2kπ+
| ||||
D、[4kπ+
|