题目内容
x2+y2+xy=1,求x+y的最小值.
考点:基本不等式
专题:不等式的解法及应用
分析:由x2+y2+xy=1,可得1=(x+y)2-xy≥(x+y)2-(
)2,化简即可得出.
| x+y |
| 2 |
解答:
解:∵x2+y2+xy=1,
∴1=(x+y)2-xy≥(x+y)2-(
)2,当且仅当x=y=
取等号.
化为(x+y)2≤
,
∴x+y≥-
.
∴x+y的最小值是-
.
∴1=(x+y)2-xy≥(x+y)2-(
| x+y |
| 2 |
| ||
| 3 |
化为(x+y)2≤
| 4 |
| 3 |
∴x+y≥-
2
| ||
| 3 |
∴x+y的最小值是-
2
| ||
| 3 |
点评:本题考查了基本不等式的性质,属于基础题.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
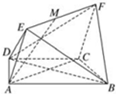 如图,在多面体ABCDEF中,四边形ABCD是梯形,AB∥CD,四边形ACFE是矩形,平面ACFE⊥平面ABCD,AD=DC=CB=a,∠ACB=
如图,在多面体ABCDEF中,四边形ABCD是梯形,AB∥CD,四边形ACFE是矩形,平面ACFE⊥平面ABCD,AD=DC=CB=a,∠ACB=