题目内容
20.已知抛物线C的顶点在坐标原点,焦点F在x轴的正半轴上,过点F的直线l与抛物线C相交于A、B两点,且满足$\overrightarrow{OA}•\overrightarrow{OB}=-\frac{3}{4}$.(1)求抛物线C的标准方程;
(2)若点M在抛物线C的准线上运动,其纵坐标的取值范围是[-1,1],且$\overrightarrow{MA}•\overrightarrow{MB}=9$,点N是以线段AB为直径的圆与抛物线C的准线的一个公共点,求点N的纵坐标的取值范围.
分析 (1)设出抛物线方程,联立方程$\left\{{\begin{array}{l}{{y^2}=2px}\\{x=ty+\frac{p}{2}}\end{array}}\right.$消去x得:y2-2pty-p2=0,利用韦达定理及向量的数量积公式,求出p,即可求抛物线的方程;
(2)由(1)知,${x_1}{x_2}=\frac{1}{4},{y_1}{y_2}=-1,{y_1}+{y_2}=2t$,结合$\overrightarrow{MA}•\overrightarrow{MB}=9$,确定t的范围,根据抛物线的定义可知,以AB为直径的圆与抛物线的准线相切,可得点N的纵坐标为$\frac{{{y_1}+{y_2}}}{2}=t$,即可求出点N的纵坐标的取值范围.
解答 解:(1)设抛物线的标准方程为y2=2px(p>0),其焦点F的坐标为$(\frac{p}{2},0)$
直线l的方程为$x=ty+\frac{p}{2}$,A(x1,y1),B(x2,y2),
联立方程$\left\{{\begin{array}{l}{{y^2}=2px}\\{x=ty+\frac{p}{2}}\end{array}}\right.$消去x得:y2-2pty-p2=0,
所以${y_1}+{y_2}=2pt,{y_1}{y_2}=-{p^2},{x_1}{x_2}=(t{y_1}+\frac{p}{2})(t{y_2}+\frac{p}{2})=\frac{p^2}{4}$,
因为$\overrightarrow{OA}•\overrightarrow{OB}={x_1}{x_2}+{y_1}{y_2}=-\frac{{3{p^2}}}{4}=-\frac{3}{4}$,解得p=1,
所以所求抛物线C的标准方程为y2=2x.
(2)设点$M(-\frac{1}{2},m),-1≤m≤1$,
由(1)知,${x_1}{x_2}=\frac{1}{4},{y_1}{y_2}=-1,{y_1}+{y_2}=2t$,所以${x_1}+{x_2}=2{t^2}+1$,
因为$\overrightarrow{MA}•\overrightarrow{MB}=({x_1}+\frac{1}{2})({x_2}+\frac{1}{2})+({y_1}-m)({y_2}-m)={(t-m)^2}$,
所以(t-m)2=9得t=m+3或t=m-3,
因为-1≤m≤1,∴2≤t≤4或-4≤t≤-2,
由抛物线定义可知,以线段AB为直径的圆与抛物线C的准线相切,
所以点N的纵坐标为$\frac{{{y_1}+{y_2}}}{2}=t$,
所以点N的纵坐标的取值范围是[-4,-2]∪[2,4].
点评 本题考查抛物线方程,考查直线与抛物线的位置关系,考查向量知识的运用,考查学生的计算能力,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | [0,3] | B. | (0,3) | C. | (-∞,0)∪(3,+∞) | D. | (-∞,0]∪[3,+∞) |

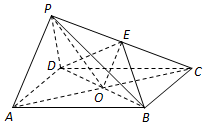 如图,在四棱锥P-ABCD中,四边形ABCD为平行四边形,AC,BD相交于点O,点E为PC的中点,OP=OC,PA⊥PD.求证:
如图,在四棱锥P-ABCD中,四边形ABCD为平行四边形,AC,BD相交于点O,点E为PC的中点,OP=OC,PA⊥PD.求证: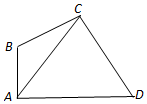 如图,在平面四边形ABCD中,AB⊥AD,AB=1,AC=$\sqrt{7}$,△ABC的面积S△ABC=$\frac{{\sqrt{3}}}{2}$,DC=$\frac{{4\sqrt{7}}}{5}$
如图,在平面四边形ABCD中,AB⊥AD,AB=1,AC=$\sqrt{7}$,△ABC的面积S△ABC=$\frac{{\sqrt{3}}}{2}$,DC=$\frac{{4\sqrt{7}}}{5}$