题目内容

8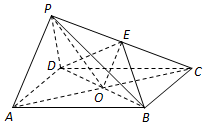．如图，在四棱锥P-ABCD中，四边形ABCD为平行四边形，AC，BD相交于点O，点E为PC的中点，OP=OC，PA⊥PD．求证：
（1）直线PA∥平面BDE；
（2）平面BDE⊥平面PCD．

分析 （1）连结OE，说明OE∥PA．然后证明PA∥平面BDE．
（2）证明OE⊥PD．OE⊥PC．推出OE⊥平面PCD．然后证明平面BDE⊥平面PCD．

解答 证明：（1）连结OE，因为O为平行四边形ABCD对角线的交点，所以O为AC中点．
又因为E为PC的中点，
所以OE∥PA．  …4分
又因为OE?平面BDE，PA?平面BDE，
所以直线PA∥平面BDE．  …6分
（2）因为OE∥PA，PA⊥PD，所以OE⊥PD．  …8分
因为OP=OC，E为PC的中点，所以OE⊥PC． …10分
又因为PD?平面PCD，PC?平面PCD，PC∩PD=P，
所以OE⊥平面PCD． …12分
又因为OE?平面BDE，所以平面BDE⊥平面PCD．  …14分．

点评 本题考查平面与平面垂直的判定定理的应用，直线与平面平行的判定定理的应用，考查空间想象能力以及逻辑推理能力．

练习册系列答案
相关题目
19．已知△ABC外接圆半径是2，$BC=2\sqrt{3}$，则△ABC的面积最大值为$3\sqrt{3}$．
20．已知抛物线C的顶点在坐标原点，焦点F在x轴的正半轴上，过点F的直线l与抛物线C相交于A、B两点，且满足$\overrightarrow{OA}•\overrightarrow{OB}=-\frac{3}{4}$．
（1）求抛物线C的标准方程；
（2）若点M在抛物线C的准线上运动，其纵坐标的取值范围是[-1，1]，且$\overrightarrow{MA}•\overrightarrow{MB}=9$，点N是以线段AB为直径的圆与抛物线C的准线的一个公共点，求点N的纵坐标的取值范围．
16．已知椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1（a＞b＞0）离心率为$\frac{\sqrt{2}}{2}$，左、右焦点分别为F1，F2，左顶点为A，|AF1|=$\sqrt{2}$-1
（Ⅰ） 求椭圆的方程；
（Ⅱ） 若直线l经过F2与椭圆交于M，N两点，求$\overrightarrow{{F_1}M}$•$\overrightarrow{{F_1}N}$取值范围．
3．抽样统计甲、乙两名学生的5次训练成绩（单位：分），结果如下：
学生第1次第2次第3次第4次第5次
甲6580708575
乙8070758070
则成绩较为稳定（方差较小）的那位学生成绩的方差为20．
13．已知向量$[\begin{array}{l}\;1\\-1\end{array}]$是矩阵A的属于特征值-1的一个特征向量．在平面直角坐标系xOy中，点P（1，1）在矩阵A对应的变换作用下变为P'（3，3），求矩阵A．
20．若实数x，y满足约束条件$\left\{\begin{array}{l}x-1≥1\\ x-y≤0\\ x+y-4≤0\end{array}\right.$，则2x+y的最大值为（　　）
A．5B．4C．6D．3
17．已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$的一个焦点为F（3，0），其左顶点A在圆O：x2+y2=12上．
（1）求椭圆C的方程；
（2）直线l：x=my+3（m≠0）交椭圆C于M，N两点，设点N关于x轴的对称点为N1（点N1与点M不重合），且直线N1M与x轴的交于点P，试问△PMN的面积是否存在最大值？若存在，求出这个最大值；若不存在，请说明理由．
18．命题“?x0∈（1，+∞），x02+2x0+2≤0”的否定形式是（　　）
A．$?x∈（1，+∞），x_0^2+2{x_0}+2＞0$B．$?x∈（{-∞，1}]，x_0^2+2{x_0}+2＞0$
C．$?{x_0}∈（1，+∞），x_0^2+2{x_0}+2＞0$D．$?{x_0}∈（{-∞，1}]，x_0^2+2{x_0}+2＞0$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网