题目内容
4.已知$\overrightarrow{AB}$⊥$\overrightarrow{AC}$,|$\overrightarrow{AB}$|=$\frac{1}{t}$,|$\overrightarrow{AC}$|=t,若P点是△ABC所在平面内一点,且$\overrightarrow{AP}$=$\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|}$+$\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|}$,当t变化时,$\overrightarrow{PB}$$•\overrightarrow{PC}$的最大值等于( )| A. | -2 | B. | 0 | C. | 2 | D. | 4 |
分析 以A为坐标原点,建立平面直角坐标系,推导出B($\frac{1}{t}$,0),C(0,t),P(1,1),从而$\overrightarrow{PB}$=($\frac{1}{t}-1$,-1),$\overrightarrow{PC}$=(-1,t-1),由此能求出$\overrightarrow{PB}$$•\overrightarrow{PC}$的最大值.
解答 解:以A为坐标原点,建立平面直角坐标系,如图所示,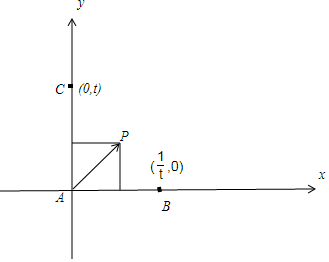
∵$\overrightarrow{AB}$⊥$\overrightarrow{AC}$,|$\overrightarrow{AB}$|=$\frac{1}{t}$,|$\overrightarrow{AC}$|=t,∴B($\frac{1}{t}$,0),C(0,t),
∵P点是△ABC所在平面内一点,且$\overrightarrow{AP}$=$\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|}$+$\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|}$,
∴$\overrightarrow{AP}$=(1,0)+(0,1)=(1,1),即P(1,1),
∴$\overrightarrow{PB}$=($\frac{1}{t}-1$,-1),$\overrightarrow{PC}$=(-1,t-1),
∴$\overrightarrow{PB}•\overrightarrow{PC}$=-$\frac{1}{t}$+1-t+1=2-($\frac{1}{t}+t$),
∵$\frac{1}{t}+t≥2\sqrt{\frac{1}{t}•t}$=2,
∴$\overrightarrow{PB}$$•\overrightarrow{PC}$的最大值等于0,
当且仅当t=$\frac{1}{t}$,即t=1时,取等号.
故选:B.
点评 本题考查向量的数量积的最大值的求法,是基础题,解题时要认真审题,注意平面向量坐标运算法则的合理运用.

 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案| A. | (0,1] | B. | [1,2] | C. | [$\frac{2}{3}$,2] | D. | [$\frac{2}{3}$,$\frac{4}{3}$] |
 在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为正方形,PA=AB,该四棱锥被一平面截去一部分后,剩余部分的三视图如图,则剩余部分体积与原四棱锥体积的比值为( )
在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为正方形,PA=AB,该四棱锥被一平面截去一部分后,剩余部分的三视图如图,则剩余部分体积与原四棱锥体积的比值为( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
| A. | $(\frac{4}{9},\frac{8}{9})$ | B. | $(\frac{2}{9},\frac{4}{9})$ | C. | (2,0) | D. | (9,0) |
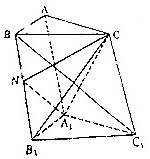 如图,在直三棱柱ABC-A1B1 C1中,AC=2$\sqrt{2}$,AB=BC=BB1=2,N是BB1的中点.
如图,在直三棱柱ABC-A1B1 C1中,AC=2$\sqrt{2}$,AB=BC=BB1=2,N是BB1的中点.