题目内容

11．已知集合A={1，2，3，4}，集合B={3，4，5，6}，则集合A∩B真子集的个数为   （　　）
A．1B．2C．3D．4

分析 利用交集定义求出A∩B，由此能求出集合A∩B真子集的个数．

解答 解：∵集合A={1，2，3，4}，集合B={3，4，5，6}，
∴A∩B={3，4}，
∴集合A∩B真子集的个数为：22-1=3．
故选：C．

点评 本题考查交集的真子集个数的求法，是基础题，解题时要认真审题，注意交集定义的合理运用．

练习册系列答案
相关题目
2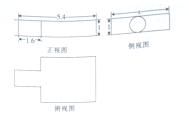．中国古代数学名著《九章算术》中记载了公元前344年商鞅制造一种标准量器-商鞅铜方升，其三视图（单位：寸）如图所示，若π取3，其体积为12.6（立方寸），则图中x的为（　　）
A．2.5B．3C．3.2D．4
3．在△ABC中，角A，B，C的对边分别为a，b，c，若a2=3b2+3c2-2$\sqrt{3}$bcsinA，则C=$\frac{π}{6}$．
20．已知抛物线C的顶点在坐标原点，焦点F在x轴的正半轴上，过点F的直线l与抛物线C相交于A、B两点，且满足$\overrightarrow{OA}•\overrightarrow{OB}=-\frac{3}{4}$．
（1）求抛物线C的标准方程；
（2）若点M在抛物线C的准线上运动，其纵坐标的取值范围是[-1，1]，且$\overrightarrow{MA}•\overrightarrow{MB}=9$，点N是以线段AB为直径的圆与抛物线C的准线的一个公共点，求点N的纵坐标的取值范围．
6．已知函数f（x）=loga（1+x），g（x）=loga（1-x），（a＞0，a≠1）
（1）若a=2，且函数f（x）的定义域为[3，36]，求f（x）的最值；
（2）求使f（x）-g（x）＞0的x的取值范围．
16．已知椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1（a＞b＞0）离心率为$\frac{\sqrt{2}}{2}$，左、右焦点分别为F1，F2，左顶点为A，|AF1|=$\sqrt{2}$-1
（Ⅰ） 求椭圆的方程；
（Ⅱ） 若直线l经过F2与椭圆交于M，N两点，求$\overrightarrow{{F_1}M}$•$\overrightarrow{{F_1}N}$取值范围．
3．抽样统计甲、乙两名学生的5次训练成绩（单位：分），结果如下：
学生第1次第2次第3次第4次第5次
甲6580708575
乙8070758070
则成绩较为稳定（方差较小）的那位学生成绩的方差为20．
20．若实数x，y满足约束条件$\left\{\begin{array}{l}x-1≥1\\ x-y≤0\\ x+y-4≤0\end{array}\right.$，则2x+y的最大值为（　　）
A．5B．4C．6D．3
1．若复数z满足i•z=$\frac{1}{2}$（1+i），则z的虚部是（　　）
A．-$\frac{1}{2}$iB．$\frac{1}{2}$iC．-$\frac{1}{2}$D．$\frac{1}{2}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网