题目内容
15.已知变量x,y满足约束条件$\left\{{\begin{array}{l}{x+y-3≥0}\\{2x-y-9≤0}\\{y≤2}\end{array}}\right.$,若使z=ax+y(a>0)取得最小值的最优解有无穷多个,则实数a=1.分析 作出不等式对应的平面区域,利用线性规划的知识,要使z=ax+y取最小值的最优解有无穷多个,则目标函数和其中一条直线平行,然后根据条件即可求出a的值.
解答 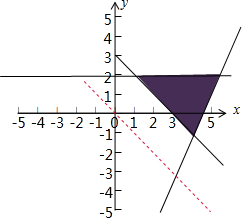 解:作出不等式组$\left\{{\begin{array}{l}{x+y-3≥0}\\{2x-y-9≤0}\\{y≤2}\end{array}}\right.$对应的平面区域如图:(阴影部分).
解:作出不等式组$\left\{{\begin{array}{l}{x+y-3≥0}\\{2x-y-9≤0}\\{y≤2}\end{array}}\right.$对应的平面区域如图:(阴影部分).
由z=ax+y,得y=-ax+z,
a>0,则目标函数的斜率k=-a<0.
平移直线y=-ax+z,
由图象可知当直线y=-ax+z和直线x+y=3平行时,此时目标函数取得最小值时最优解有无数多个,
此时-a=-1,即a=1.
故答案为:1.
点评 本题主要考查线性规划的应用,利用数形结合是解决此类问题的基本方法,利用z的几何意义是解决本题的关键.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
5.给出下列四个命题:
①已知m,n是常数,“mn<0”是“mx2+ny2=1表示双曲线的充分不必要条件”;
②命题p:“?x∈R,sinx≤1”的否定是¬p:“?x0∈R,sinx0>1”;
③已知命题p和q,若p∨q是假命题,则p与q中必一真一假;
④命题“若a>b>0,则a2>b2”的逆命题是假命题.
其中真命题的序号是( )
①已知m,n是常数,“mn<0”是“mx2+ny2=1表示双曲线的充分不必要条件”;
②命题p:“?x∈R,sinx≤1”的否定是¬p:“?x0∈R,sinx0>1”;
③已知命题p和q,若p∨q是假命题,则p与q中必一真一假;
④命题“若a>b>0,则a2>b2”的逆命题是假命题.
其中真命题的序号是( )
| A. | ①②④ | B. | ①③④ | C. | ②④ | D. | ②③ |
6.函数$f(x)=-x+\frac{1}{x}$在$[{-2,-\frac{1}{3}}]$上的最大值是( )
| A. | $\frac{3}{2}$ | B. | $-\frac{8}{3}$ | C. | -2 | D. | 2 |
10.将函数f(x)=sin3x+cos3x的图象沿x轴向左平移∅个单位后,得到一个偶函数的图象,则∅的一个可能取值为( )
| A. | $\frac{π}{12}$ | B. | $-\frac{π}{12}$ | C. | $\frac{π}{4}$ | D. | 0 |
3.抽样统计甲、乙两名学生的5次训练成绩(单位:分),结果如下:
则成绩较为稳定(方差较小)的那位学生成绩的方差为20.
| 学生 | 第1次 | 第2次 | 第3次 | 第4次 | 第5次 |
| 甲 | 65 | 80 | 70 | 85 | 75 |
| 乙 | 80 | 70 | 75 | 80 | 70 |
4.执行如图所示的程序框图后,输出的值为4,则p的取值范围是( )


| A. | $\frac{3}{4}<p≤\frac{7}{8}$ | B. | $p>\frac{5}{16}$ | C. | $\frac{7}{8}≤p<\frac{5}{16}$ | D. | $\frac{7}{8}<p≤\frac{5}{16}$ |