题目内容
11．已知$cos（{\frac{π}{6}-α}）=\frac{{\sqrt{3}}}{3}$，则$sin（{\frac{π}{3}+α}）$=$\frac{\sqrt{3}}{3}$．分析 利用诱导公式即可得出．
解答 解：∵$cos（{\frac{π}{6}-α}）=\frac{{\sqrt{3}}}{3}$，则$sin（{\frac{π}{3}+α}）$=$cos（{\frac{π}{6}-α}）=\frac{{\sqrt{3}}}{3}$，
故答案为：$\frac{{\sqrt{3}}}{3}$．
点评 本题考查了诱导公式，考查了推理能力与计算能力，属于基础题．
练习册系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
1．在投篮测试中，每人投3次，其中至少有两次投中才能通过测试．已知某同学每次投篮投中的概率为0.6，且各次投篮是否投中相互独立，则该同学能通过测试的概率为（ ）
| A． | 0.352 | B． | 0.432 | C． | 0.36 | D． | 0.648 |
2．
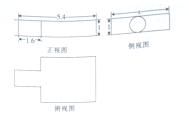中国古代数学名著《九章算术》中记载了公元前344年商鞅制造一种标准量器-商鞅铜方升，其三视图（单位：寸）如图所示，若π取3，其体积为12.6（立方寸），则图中x的为（ ）
中国古代数学名著《九章算术》中记载了公元前344年商鞅制造一种标准量器-商鞅铜方升，其三视图（单位：寸）如图所示，若π取3，其体积为12.6（立方寸），则图中x的为（ ）| A． | 2.5 | B． | 3 | C． | 3.2 | D． | 4 |
6．函数$f（x）=-x+\frac{1}{x}$在$[{-2，-\frac{1}{3}}]$上的最大值是（ ）
| A． | $\frac{3}{2}$ | B． | $-\frac{8}{3}$ | C． | -2 | D． | 2 |
16．函数f（x）=sin2x+2$\sqrt{3}$cos2x-$\sqrt{3}$，函数g（x）=mcos（2x-$\frac{π}{6}$）-2m+3（m＞0），若存在x1，x2∈[0，$\frac{π}{4}$]，使得f（x1）=g（x2）成立，则实数m的取值范围是（ ）
| A． | （0，1] | B． | [1，2] | C． | [$\frac{2}{3}$，2] | D． | [$\frac{2}{3}$，$\frac{4}{3}$] |