题目内容
已知函数f（x）=x-
，则（ ）
| 1 |
| x |
| A、函数f（x）的定义域是R |
| B、函数f（x）的值域是（-∞，0）∪（0，+∞） |
| C、函数f（x）在其定义域内是奇函数 |
| D、函数f（x）在其定义域内是增函数 |
考点：函数奇偶性的判断
专题：函数的性质及应用
分析：根据函数成立的条件，即可求出函数的定义域和单调性，
解答：
解：要使函数有意义，则x≠0，则函数的定义域为{x|x≠0}，
∵f（-x）=-x+
=-（x-
）=-f（x），
∴函数f（x）是奇函数，
故选：C．
∵f（-x）=-x+
| 1 |
| x |
| 1 |
| x |
∴函数f（x）是奇函数，
故选：C．
点评：本题主要考查函数奇偶性和定义域的求法，比较基础．
练习册系列答案
相关题目
集合A={x|x2＞1}，B={x|x+a≥0}，若∁UA⊆B，则实数a的取值范围是（ ）
| A、[-1，+∞） |
| B、[1，+∞） |
| C、（-∞，1] |
| D、（-∞，-1] |
某校高三年级从一次模拟考试中随机抽取50名学生（男、女生各25名），将数学成绩进行统计，所得数据的茎叶图如图所示，以组距为10将数据按[80，90），[90，100），…，[130，140），[140，150]分成七组绘制频率分布直方图，则落在区间[130，140）的小矩形的面积为（ ）| A、1.2 | B、6 |
| C、0012 | D、0.12 |
已知定义在（0，+∞）上的单调函数f（x），对?x∈（0，+∞），都有f[f（x）-log3 x]=4，则函数g（x）=f（x-1）-f′（x-1）-3的零点所在区间是（ ）
| A、（1，2） | ||
| B、（2，3） | ||
C、（
| ||
D、（0，
|
执行如下的程序框图，如果输入M的值是6，那么输出的n值是（ ）
| A、5040 | B、1440 |
| C、720 | D、120 |
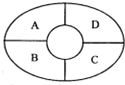如图某综艺节目现场设有A、B、C、D四个观众席，现有由3中不同颜色与2种不同款式组成的6中马甲安排给现场观众，要求每个观众席上的马甲相同，相邻观众席上的马甲的颜色与款式都不相同，则不同的安排方法种数为（ ）