题目内容
已知直线ax-by-3=0与f（x）=xex在点P（1，e）处的切线相互垂直，则
= ．
| a |
| b |
考点：利用导数研究曲线上某点切线方程
专题：导数的综合应用
分析：由导数的几何意义可求曲线f（x）=xex在（1，e）处的切线斜率k，然后根据直线垂直的条件可求
的值．
| a |
| b |
解答：
解：设曲线f（x）=xex在点P（1，e）处的切线斜率为k，
由f（x）=xex，得f′（x）=ex+xex，
则k=f′（1）=2e，
∵直线ax-by-2=0与曲线f（x）=xex在点P（1，e）处的切线互相垂直．
∴
=-
．
故答案为：-
．
由f（x）=xex，得f′（x）=ex+xex，
则k=f′（1）=2e，
∵直线ax-by-2=0与曲线f（x）=xex在点P（1，e）处的切线互相垂直．
∴
| a |
| b |
| 1 |
| 2e |
故答案为：-
| 1 |
| 2e |
点评：本题主要考查了导数的几何意义：曲线在点（x0，y0）处的切线斜率即为该点处的导数值，两直线垂直的条件的运用．属于中档题．
练习册系列答案
相关题目
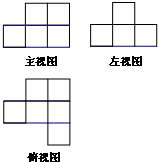在一个仓库里堆积着正方体的货箱若干，要搬运这些箱子很困难，可是仓库管理员要清点一下箱子的数量，于是就想出一个办法：将这堆货物的三视图画了出来，你能根据三视图，帮他清点一下箱子的数量吗？这些正方体货箱的个数为（ ）| A、6 | B、7 | C、8 | D、9 |
（理科） 为了近似求出圆周率的值，有人设计如下方法来进行随机模拟：如图，双曲线某几何体三视图如下图所示，则该几何体的表面积为（ ）
| A、16-π | B、16+π |
| C、16-2π | D、16+2π |
已知集合M={x|
≤1}，N={x|y=lg（1-x）}，则下列关系中正确的是（ ）
| 1 |
| x |
| A、（∁RM）∩N=∅ |
| B、M∪N=R |
| C、M?N |
| D、（∁RM）∪N=R |