题目内容

已知函数f（x）=
log2x，x＞0
3x，x≤0
 则f（f（
1
4
））=
 
．
考点：函数的值
专题：函数的性质及应用
分析：由此得f（
1
4
）=log2
1
4
=-2，由此能求出f（f（
1
4
））．
解答： 解：∵函数f（x）=
log2x，x＞0
3x，x≤0
，
∴f（
1
4
）=log2
1
4
=-2，
f（f（
1
4
））=f（-2）=3-2=
1
9
．
故答案为：
1
9
．
点评：本题考查函数值的求法，是基础题，解题时要认真审题，注意分段函数的性质的合理运用．
练习册系列答案
相关题目
设集合A={x|x2-3x-4＞0}，B={x|-2≤x≤3}，则A∩B=（　　）
A、R
B、（-1，3]
C、[-2，-1）
D、[-2，4]
已知函数f（x）=x2+ax+3若f（x）在区间[1，4]上为单调函数，则a的范围是
 
；
变式为：已知函数f（x）=x2+ax+3
（1）若y=f（x）在区间[1，4]有最大值10，则a的值为
 
；
（2）若f（x）=0在区间[1，4]内有两个不相等的实根，则a的范围为
 
．；
（3）若f（x）=0在区间[1，4]内有解．则a的范围为
 
；
（4）若y=f（x）在区间[1，4]内存在x0，使f（x0）＞0，则a的范围为
 
；
（5）若y=f（x）在区间[1，4]上恒为正数，则a的范围为
 
；
（6）设A={x|f（x）≤0}，B=[1，4]，若A≠B且A∩B=A，则a的范围为
 
；
（7）设A={x|f（x）≤0}，B=[1，4]，若B⊆A，则a的范围为
 
．
已知函数f（x）=
a
x+2
（x∈R且x≠-2）．
（Ⅰ）函数y=f（x）图象是否是中心对称图形，如果是求出其对称中心，并给予证明；如果不是请说出理由．（Ⅱ）当a=-1时，数列{an}满足a1=-
1
2
，an+1=f（an）．
①求数列{an}的通项；
②求证：（2-an）n+1（-an）n＞1．
若不等式组
x-y+3≥0  
y≥a  
0≤x≤3  
表示的平面区域是一个三角形，则a的取值范围是（　　）
A、[0，3]
B、[0，3）
C、[3，6）
D、[3，6]
等差数列{an}的前n项和为Sn，已知a1=10，a2为整数，且在前n项和中S4最大．
（Ⅰ）求{an}的通项公式；
（Ⅱ）设bn=
13-an
3n+1
，n∈N*．
（1）求证：bn+1＜bn≤
1
3
； 
（2）求数列{b2n}的前n项和Tn．
已知直线ax-by-3=0与f（x）=xex在点P（1，e）处的切线相互垂直，则
a
b
=
 
．
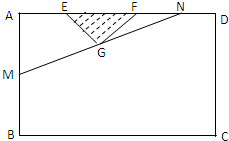某小区想利用一矩形空地ABCD建造市民健身广场，设计时决定保留空地边上的一个水塘（如图中阴影部分），水塘可近似看作一个等腰直角三角形，其中AD=60m，AB=40m，且△EFG中，∠EGF=90°，经测量得到AE=10m，EF=20m．为保证安全同时考虑美观，健身广场周围准备加设一个保护栏．设计时经过点G作一条直线交AB，DF于M，N，从而得到五边形MBCDN的市民健身广场．
（Ⅰ）假设DN=x（m），试将五边形MBCDN的面积y表示为x的函数，并注明函数的定义域；
（Ⅱ）问：应如何设计，可使市民健身广场的面积最大？并求出健身广场的最大面积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网