题目内容
已知函数f（x）=x2+mx-2n，m，n∈[0，2]，则使f（1）≤0成立的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：几何概型
专题：概率与统计
分析：本题利用几何概型求解即可．在坐标系中，画出f（1）≤0对应的区域，m，n都是在区间[0，2]内，计算它们区域的面积的比值即得．
解答：
解：f（1）=1+m-2n≤0，即2n-m＞1，
如图，
A（0，1），B（2，1.5），C（2，2），D（0，2）
S四边形ABCD=
(
+
)×2=2，P=
=
=
．
故选B．
如图，
A（0，1），B（2，1.5），C（2，2），D（0，2）
S四边形ABCD=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| S四边形ABCD |
| S正方形 |
| 2 |
| 4 |
| 1 |
| 2 |
故选B．
点评：本题主要考查几何概型．如果每个事件发生的概率只与构成该事件区域的长度（面积或体积）成比例，则称这样的概率模型为几何概率模型，简称为几何概型．
练习册系列答案
导学教程高中新课标系列答案
相关题目
设a、b是两条不同的直线，α、β是两个不同的平面，则下面四个命题中错误的是（ ）
| A、若a⊥b，a⊥α，b?α，则b∥α |
| B、若a⊥b，a⊥α，b⊥β，则α⊥β |
| C、若a⊥β，α⊥β，则a∥α或a?α |
| D、若 a∥α，α⊥β，则a⊥β |
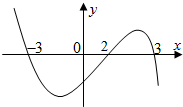若连续函数f（x）在R上可导，其导函数为f′（x），且函数y=（2-x）f′（x）的图象如图所示，则下列结论中一定成立的是（ ）| A、f（x）有极大值f（3）和极小值f（2） |
| B、f（x）有极大值f（-3）和极小值f（2） |
| C、f（x）有极大值f（3）和极小值f（-3） |
| D、f（x）有极大值f（-3）和极小值f（3） |
已知数列{an}的首项a1=1，an+1=3Sn(n∈N*)，则下列结论正确的是（ ）
| A、数列是{an}等比数列 |
| B、数列a2，a3，…，an是等比数列 |
| C、数列是{an}等差数列 |
| D、数列a2，a3，…，an是等差数列 |
下列命题错误的是（ ）
| A、命题“若m＞0，则方程x2+x-m=0有实根”的逆否命题为：“若方程x2+x-m=0无实根，则m≤0”； | ||||||||||||||||
| B、“x=1”是“x2-3x+2=0”的充分不必要条件； | ||||||||||||||||
| C、命题p：?x0∈R，|sinx0|＞1，则￢p：对?x∈R，|sinx|≤1； | ||||||||||||||||
D、命题“若
|
某程序框图如下图所示，则该程序运行后输出S的值为（ ）
| A、10 | B、12 | C、15 | D、18 |