题目内容
在△ABC中,已知∠BAC=150°,且
•
=-4
,设D是△ABC内部的一点,△DAB、△DBC、△DCA的面积依次为m、n、p,则当p=1时,
+
的最小值为( )
| AB |
| AC |
| 3 |
| 1 |
| m |
| 4 |
| n |
| A、3 | B、5 | C、7 | D、9 |
考点:平面向量数量积的运算
专题:计算题,解三角形,不等式的解法及应用,平面向量及应用
分析:运用数量积的定义,求得|
|•|
|=8,再由三角形的面积公式,求得△ABC的面积,再由m+n=1,则
+
=(m+n)(
+
),化简整理,运用基本不等式即可得到最小值.
| AB |
| AC |
| 1 |
| m |
| 4 |
| n |
| 1 |
| m |
| 4 |
| n |
解答:
解:∠BAC=150°,且
•
=-4
,
则|
|•|
|•cos150°=-
|
|•|
|=-4
,
即有|
|•|
|=8,
则有S△ABC=
|
|•|
|•sin150°=
×8×
=2,
由于m+n+p=2,p=1,则m+n=1,
则
+
=(m+n)(
+
)=5+(
+
)
≥5+2
=9.
当且仅当n=2m=
,取得最小值9.
故选D.
| AB |
| AC |
| 3 |
则|
| AB |
| AC |
| ||
| 2 |
| AB |
| AC |
| 3 |
即有|
| AB |
| AC |
则有S△ABC=
| 1 |
| 2 |
| AB |
| AC |
| 1 |
| 2 |
| 1 |
| 2 |
由于m+n+p=2,p=1,则m+n=1,
则
| 1 |
| m |
| 4 |
| n |
| 1 |
| m |
| 4 |
| n |
| n |
| m |
| 4m |
| n |
≥5+2
|
当且仅当n=2m=
| 2 |
| 3 |
故选D.
点评:本题考查平面向量的数量积的定义,考查三角形的面积公式以及基本不等式的运用:求最值,考查运算能力,属于中档题和易错题.

练习册系列答案
相关题目
设f(x)=
+2x,0<a<b<e,则( )
| lnx |
| x |
| A、f(a)>f(b) |
| B、f(a)<f(b) |
| C、f(a)=f(b) |
| D、f(a)f(b)>0 |
设a、b是两条不同的直线,α、β是两个不同的平面,则下面四个命题中错误的是( )
| A、若a⊥b,a⊥α,b?α,则b∥α |
| B、若a⊥b,a⊥α,b⊥β,则α⊥β |
| C、若a⊥β,α⊥β,则a∥α或a?α |
| D、若 a∥α,α⊥β,则a⊥β |
设函数g(x)满足g(x+2)=g(2-x),f(x)=
,若关于x的方程f2(x)+bf(x)+c=0有三个不同的实数解x1,x2,x3,则x1+x2+x3=( )
|
| A、0 | B、2 | C、4 | D、6 |
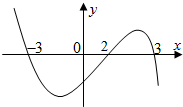 若连续函数f(x)在R上可导,其导函数为f′(x),且函数y=(2-x)f′(x)的图象如图所示,则下列结论中一定成立的是( )
若连续函数f(x)在R上可导,其导函数为f′(x),且函数y=(2-x)f′(x)的图象如图所示,则下列结论中一定成立的是( )| A、f(x)有极大值f(3)和极小值f(2) |
| B、f(x)有极大值f(-3)和极小值f(2) |
| C、f(x)有极大值f(3)和极小值f(-3) |
| D、f(x)有极大值f(-3)和极小值f(3) |
已知数列{an}的首项a1=1,an+1=3Sn(n∈N*),则下列结论正确的是( )
| A、数列是{an}等比数列 |
| B、数列a2,a3,…,an是等比数列 |
| C、数列是{an}等差数列 |
| D、数列a2,a3,…,an是等差数列 |
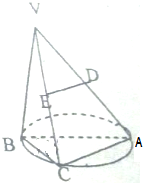 如图,AB是圆O的直径,AB=2,点C在圆O上,且∠ABC=60°,V到圆O所在的平面的距离为3,且VC垂直于圆O所在的平面,D,E分别是VA,VC的中点.
如图,AB是圆O的直径,AB=2,点C在圆O上,且∠ABC=60°,V到圆O所在的平面的距离为3,且VC垂直于圆O所在的平面,D,E分别是VA,VC的中点.