题目内容
解方程x log3xloga3=
，x= ．
| x2 |
| a |
考点：对数的运算性质
专题：计算题
分析：根据对数，指数幂的运算性质得出xlogax=
，两边取对数得出：loga2x-2logax+1=0，化简得出logax=1，即可求解．
| x2 |
| a |
解答：
解：∵xlo
lo
=
，
∴xlogax=
，
∴两边取对数得出：loga2x-2logax+1=0
logax=1，
∴x=a，
故答案为：a
| g | x 3 |
| g | 3 a |
| x2 |
| a |
∴xlogax=
| x2 |
| a |
∴两边取对数得出：loga2x-2logax+1=0
logax=1，
∴x=a，
故答案为：a
点评：本题考查了对数的运用算，二次方程的求解，属于计算题，难度较大，注意化简．
练习册系列答案
相关题目
使得(x+
)n（n∈N*）的展开式中含有常数项的最小的n是（ ）
| 1 | ||
x
|
| A、4 | B、5 | C、6 | D、7 |
设a、b是两条不同的直线，α、β是两个不同的平面，则下面四个命题中错误的是（ ）
| A、若a⊥b，a⊥α，b?α，则b∥α |
| B、若a⊥b，a⊥α，b⊥β，则α⊥β |
| C、若a⊥β，α⊥β，则a∥α或a?α |
| D、若 a∥α，α⊥β，则a⊥β |
若正数a，b，c成公差不为零的等差数列，则（ ）
| A、lga，lgb，lgc成等差数列 |
| B、lga，lgb，lgc成等比数列 |
| C、2a，2b，2c成等差数列 |
| D、2a，2b，2c成等比数列 |
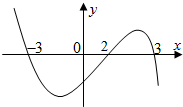若连续函数f（x）在R上可导，其导函数为f′（x），且函数y=（2-x）f′（x）的图象如图所示，则下列结论中一定成立的是（ ）| A、f（x）有极大值f（3）和极小值f（2） |
| B、f（x）有极大值f（-3）和极小值f（2） |
| C、f（x）有极大值f（3）和极小值f（-3） |
| D、f（x）有极大值f（-3）和极小值f（3） |
已知集合A={0，1，2}，B={1，4}，那么集合A∩B等于（ ）
| A、{1} |
| B、{4} |
| C、{2，3} |
| D、{1，2，3，4} |