题目内容
对于给定数列{cn},如果存在实常数p,q使得cn+1=pcn+q对于任意n∈N*都成立,我们称数列{cn}是“线性数列”.
(1)若an=2n,bn=3•2n,n∈N*,数列{an}、{bn}是否为“线性数列”?若是,指出它对应的实常数p&,q,若不是,请说明理由;
(2)证明:若数列{an}是“线性数列”,则数列{an+an+1}也是“线性数列”;
(3)若数列{an}满足a1=2,an+an+1=3t•2n(n∈N*),t为常数.求数列{an}前n项的和.
(1)若an=2n,bn=3•2n,n∈N*,数列{an}、{bn}是否为“线性数列”?若是,指出它对应的实常数p&,q,若不是,请说明理由;
(2)证明:若数列{an}是“线性数列”,则数列{an+an+1}也是“线性数列”;
(3)若数列{an}满足a1=2,an+an+1=3t•2n(n∈N*),t为常数.求数列{an}前n项的和.
考点:数列的求和,数列递推式
专题:等差数列与等比数列
分析:(1)an=2n,则an+1=an+2,n∈N*,可得数列{an}是“线性数列”,对应的实常数分别为1,2.同理数列{bn}是“线性数列”.
(2)利用“线性数列”的定义即可证明;
(3)对n分奇数与偶数讨论,利用等比数列的前n项和公式即可得出.
(2)利用“线性数列”的定义即可证明;
(3)对n分奇数与偶数讨论,利用等比数列的前n项和公式即可得出.
解答:
(1)解:∵an=2n,则an+1=an+2,n∈N*,
∴数列{an}是“线性数列”,对应的实常数分别为1,2.
∵bn=3•2n,则有bn+1=2bn,n∈N*,
∴数列{bn}是“线性数列”,对应的实常数分别为2,0.
(2)证明:若数列{an}是“线性数列”,则存在实常数p,q,
使得an+1=pan+q对于任意n∈N*都成立,
且有an+2=pan+1+q对于任意n∈N*都成立,
因此(an+1+an+2)=p(an+an+1)+2q对于任意n∈N*都成立,
故数列{an+an+1}也是“线性数列”.
对应的实常数分别为p,2q.
(3)解:∵an+an+1 =3t•2n (n∈N*),
当n为偶数时,Sn=(a1+a2)+(a3+a4)+…+(an-1+an)
=3t•2+3t•22+…3t•2n-1
=3t(2+22+…+2n-1)=3t•
=t•2n+1-2t.
当n为奇数时,Sn=a1+(a2+a3)+(a4+a5)+…+(an-1+an)
=2+3t•22+3t•24+…+3t•2n-1=2+3t•(22+24+…+2n-1)
=2+3t•
=t•2n+1-4t+2.
故数列{an}前n项的和Sn=
….
∴数列{an}是“线性数列”,对应的实常数分别为1,2.
∵bn=3•2n,则有bn+1=2bn,n∈N*,
∴数列{bn}是“线性数列”,对应的实常数分别为2,0.
(2)证明:若数列{an}是“线性数列”,则存在实常数p,q,
使得an+1=pan+q对于任意n∈N*都成立,
且有an+2=pan+1+q对于任意n∈N*都成立,
因此(an+1+an+2)=p(an+an+1)+2q对于任意n∈N*都成立,
故数列{an+an+1}也是“线性数列”.
对应的实常数分别为p,2q.
(3)解:∵an+an+1 =3t•2n (n∈N*),
当n为偶数时,Sn=(a1+a2)+(a3+a4)+…+(an-1+an)
=3t•2+3t•22+…3t•2n-1
=3t(2+22+…+2n-1)=3t•
2(1-4
| ||
| 1-4 |
当n为奇数时,Sn=a1+(a2+a3)+(a4+a5)+…+(an-1+an)
=2+3t•22+3t•24+…+3t•2n-1=2+3t•(22+24+…+2n-1)
=2+3t•
4(1-4
| ||
| 1-4 |
故数列{an}前n项的和Sn=
|
点评:本题考查了线性数列”的定义、等比数列的前n项和公式,考查了分类讨论的思想方法,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
使得(x+
)n(n∈N*)的展开式中含有常数项的最小的n是( )
| 1 | ||
x
|
| A、4 | B、5 | C、6 | D、7 |
设a、b是两条不同的直线,α、β是两个不同的平面,则下面四个命题中错误的是( )
| A、若a⊥b,a⊥α,b?α,则b∥α |
| B、若a⊥b,a⊥α,b⊥β,则α⊥β |
| C、若a⊥β,α⊥β,则a∥α或a?α |
| D、若 a∥α,α⊥β,则a⊥β |
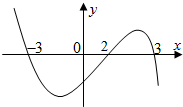 若连续函数f(x)在R上可导,其导函数为f′(x),且函数y=(2-x)f′(x)的图象如图所示,则下列结论中一定成立的是( )
若连续函数f(x)在R上可导,其导函数为f′(x),且函数y=(2-x)f′(x)的图象如图所示,则下列结论中一定成立的是( )| A、f(x)有极大值f(3)和极小值f(2) |
| B、f(x)有极大值f(-3)和极小值f(2) |
| C、f(x)有极大值f(3)和极小值f(-3) |
| D、f(x)有极大值f(-3)和极小值f(3) |
下列命题错误的是( )
| A、命题“若m>0,则方程x2+x-m=0有实根”的逆否命题为:“若方程x2+x-m=0无实根,则m≤0”; | ||||||||||||||||
| B、“x=1”是“x2-3x+2=0”的充分不必要条件; | ||||||||||||||||
| C、命题p:?x0∈R,|sinx0|>1,则¬p:对?x∈R,|sinx|≤1; | ||||||||||||||||
D、命题“若
|
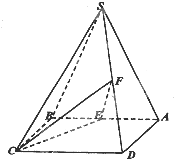 如图,四棱锥S-ABCD的底面ABCD是正方形,侧面SAB是等腰三角形且垂直于底面,SA=SB=
如图,四棱锥S-ABCD的底面ABCD是正方形,侧面SAB是等腰三角形且垂直于底面,SA=SB=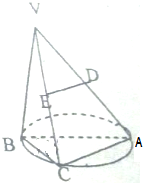 如图,AB是圆O的直径,AB=2,点C在圆O上,且∠ABC=60°,V到圆O所在的平面的距离为3,且VC垂直于圆O所在的平面,D,E分别是VA,VC的中点.
如图,AB是圆O的直径,AB=2,点C在圆O上,且∠ABC=60°,V到圆O所在的平面的距离为3,且VC垂直于圆O所在的平面,D,E分别是VA,VC的中点.