题目内容
已知椭圆 过点
过点 ,离心率为
,离心率为 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)过点 且斜率为
且斜率为 (
( )的直线
)的直线 与椭圆
与椭圆 相交于
相交于 两点,直线
两点,直线 ,
, 分别交直线
分别交直线 于
于 ,
, 两点,线段
两点,线段 的中点为
的中点为 .记直线
.记直线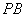 的斜率为
的斜率为 ,求证:
,求证:  为定值.
为定值.
解:(Ⅰ)依题得 解得
解得 ,
, .
.
所以椭圆 的方程为
的方程为 .
.
(Ⅱ)根据已知可设直线 的方程为
的方程为 .
.
由 得
得 .
.
设 ,则
,则 .
.
直线 ,
, 的方程分别为:
的方程分别为: ,
,
令 ,
,
则 ,所以
,所以 .
.
所以


 .
. 

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
 的最大值是 。
的最大值是 。




 中,点
中,点 是半圆
是半圆 (
( ≤
≤ ≤
≤ 的延长线上.当
的延长线上.当 时,则点
时,则点 (D)
(D) 

 ,
, .
. ,且
,且 求a,b的值;
求a,b的值; 的单调区间,并求该函数在区间(-2,m] (
的单调区间,并求该函数在区间(-2,m] ( )上的最大值。
)上的最大值。
 的最小正周期和单调递增区间;
的最小正周期和单调递增区间; 上的值域.
上的值域. ,
, ,
, ,则
,则 ( )
( )
 B.
B. C.
C. D.
D.