Question

已知函数，.

(1)设函数，且求a,b的值；

(2)当a=2且b=4时，求函数的单调区间，并求该函数在区间（-2，m] （）上的最大值。

Answer 1

解：(Ⅰ)函数h(x)定义域为{x|x≠-a}，

则，

因为所以解得，或

 (Ⅱ)记(x)= ，则(x)=(x+a)(bx²+3x)(x≠-a) ,

因为a=2，b=4，所以(x≠-2),

,

令，得，或, 

当，或时，，当时，，

函数的单调递增区间为，

单调递减区间为,

①当-2<m<时，(x)在（-2，m）上单调递增，

其最大值为(m)= ， 

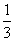②当≤m≤时，(x)在（-2，）上单调递增，在（，-）上单调递减，在（，m）上单调递增，而()=()=，

(x)的最大值为.