题目内容
2.an+1=3an+2n+3,a1=1,求数列{an}的通项公式.分析 由已知推导出$\frac{{a}_{n+1}}{{2}^{n+3}}$+2=$\frac{3}{2}$($\frac{{a}_{n}}{{2}^{n+2}}$+2),从而数列{$\frac{{a}_{n}}{{2}^{n+3}}$+2}是首项为$\frac{{a}_{1}}{{2}^{3}}$+2=$\frac{17}{8}$,公比为$\frac{3}{2}$的等比数列,由此能求出数列{an}的通项公式.
解答 解:∵an+1=3an+2n+3,a1=1,
两端同除以2n+3得,$\frac{{a}_{n+1}}{{2}^{n+3}}=\frac{3}{2}•\frac{{a}_{n}}{{2}^{n+1}}+1$,
∴$\frac{{a}_{n+1}}{{2}^{n+3}}$+2=$\frac{3}{2}$($\frac{{a}_{n}}{{2}^{n+2}}$+2),
∴数列{$\frac{{a}_{n}}{{2}^{n+3}}$+2}是首项为$\frac{{a}_{1}}{{2}^{3}}$+2=$\frac{17}{8}$,公比为$\frac{3}{2}$的等比数列,
故$\frac{{a}_{n}}{{2}^{n+2}}$+2=$\frac{17}{8}$×($\frac{3}{2}$)n-1,
∴an=17×3n-1-2n+3.
点评 本题考查数列的通项公式的求法,是中档题,解题时要认真审题,注意构造法的合理运用.

练习册系列答案
相关题目
7.命题?x∈R,cosx≤1的真假判断及其否定是( )
| A. | 真,?x0∈R,cosx0>1 | B. | 真,?x∈R,cosx>1 | ||
| C. | 假,?x0∈R,cosx0>1 | D. | 假,?x∈R,cosx>1 |
12.已知(1+x)10=a0+a1(1-x)+a2(1-x)2+…+a10(1-x)10,则a1+a2+…+a9=( )
| A. | 1 | B. | 1024 | C. | -1024 | D. | -2015 |
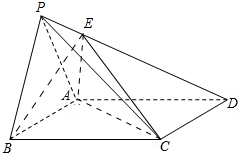 如图,在四棱锥P-ABCD中,底面ABCD为正方形,平面PAD⊥平面ABCD,点E在棱PD上,且AE⊥PD
如图,在四棱锥P-ABCD中,底面ABCD为正方形,平面PAD⊥平面ABCD,点E在棱PD上,且AE⊥PD