Question

13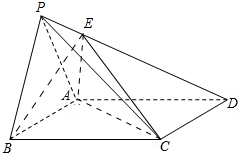．如图，在四棱锥P-ABCD中，底面ABCD为正方形，平面PAD⊥平面ABCD，点E在棱PD上，且AE⊥PD
（1）求证：AB⊥平面PAD；
（2）求证：平面ABE⊥平面PCD．

Answer 1

分析 （1）推导出AB⊥AD，由平面PAD⊥平面ABCD，平面PAD∩平面ABCD=AD，能证明AB⊥平面PAD．
（2）推导出AE⊥CD，AE⊥PD，从而AE⊥平面PCD，由此能证明平面ABE⊥平面PCD．

解答 证明：（1）∵底面ABCD为正方形，
∴AB⊥AD，
∵平面PAD⊥平面ABCD，平面PAD∩平面ABCD=AD，
∴AB⊥平面PAD．
（2）∵AB⊥平面PAD，底面ABCD为正方形，∴CD⊥平面PAD，
∵AE?平面PAD，∴AE⊥CD，
∵点E在棱PD上，且AE⊥PD，PD∩CD=D，
∴AE⊥平面PCD，
∵AE?平面ABE，∴平面ABE⊥平面PCD．

点评 本题考查线面垂直的证明，考查面面垂直的证明，是中档题，解题时要认真审题，注意空间思维能力的培养．