题目内容
如图，在以AE=2为直径的半圆周上，B、C，D分别为弧AE的四等分点．（Ⅰ）在弧AE上随机取一点P，求满足
| OP |
| OA |
| ||
| 2 |
（Ⅱ）在以O为起点，再从A，B，C，D，E这5个点中任取两点分别为终点得到两个向量，记这两向量数量积为x，则x=
| ||
| 2 |
考点：平面向量数量积的含义与物理意义,列举法计算基本事件数及事件发生的概率
专题：概率与统计
分析：（1）根据概率定义，计算即可，
（2）通过列举法，列出所有满足条件的向的基本事件量，然后观察符合条件的基本事件，计算即可．
（2）通过列举法，列出所有满足条件的向的基本事件量，然后观察符合条件的基本事件，计算即可．
解答：
解：（Ⅰ）由题知|
|cos∠AOP＞
，
则0≤∠AOP＜
，
∴使得
在
上的射影大于
的概率P=
=
，
（Ⅱ）以O点为起点，从A，B，C，D，E，这5个点中任取两点分别为终点得到两个向量所有的基本事件有：
(
，
)，(
，
)，(
，
)，(
，
)，(
，
)，
(
，
)，(
，
)，(
，
，(
，
)，(
，
)，
其中数量积x=
的有：(
，
)，(
，
)，(
，
)，(
，
)．
则P(x=
)=
．
| OP |
| ||
| 2 |
则0≤∠AOP＜
| π |
| 4 |
∴使得
| OP |
| OA |
| 1 |
| 2 |
| ||
| π |
| 1 |
| 4 |
（Ⅱ）以O点为起点，从A，B，C，D，E，这5个点中任取两点分别为终点得到两个向量所有的基本事件有：
(
| OA |
| OB |
| OA |
| OC |
| OA |
| OD |
| OA |
| OE |
| OB |
| OC |
(
| OB |
| OD |
| OB |
| OE |
| OC |
| OD) |
| OC |
| OE |
| OD |
| OE |
其中数量积x=
| ||
| 2 |
| OA |
| OB |
| OB |
| OC |
| OC |
| OD |
| OD |
| OE |
则P(x=
| ||
| 2 |
| 2 |
| 5 |
点评：本题主要考查了概率的求法以及向量的有关知识，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
若二项式（
+x2）3展开式中的常数项为k，则直线y=kx与曲线y=x2围成的封闭图形的面积为（ ）
| 1 |
| x |
| A、3 | ||
B、
| ||
| C、9 | ||
D、
|
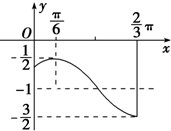如图，是函数y=Asin（ωx+φ）+k（A＞0，ω＞0，|φ|＜
某学校为了选拔学生参加“XX市中学生知识竞赛”，先在本校进行选拔测试（满分150分），若该校有100名学生参加选拔测试，并根据选拔测试成绩作出如图所示的频率分布直方图．