Question

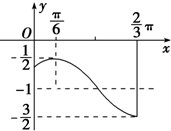如图，是函数y=Asin（ωx+φ）+k（A＞0，ω＞0，|φ|＜

π

2

）的一段图象．
（1）写出此函数的解析式；
（2）求该函数的对称轴方程和对称中心坐标．

Answer 1

考点：由y=Asin（ωx+φ）的部分图象确定其解析式,正弦函数的图象,函数y=Asin（ωx+φ）的图象变换

专题：三角函数的图像与性质

分析：（1）通过图象求出函数的振幅，求出周期推出ω，利用函数经过的特殊点求出φ，即可写出此函数的解析式；
（2）利用正弦函数的对称中心以及对称轴方程，直接求该函数的对称轴方程和对称中心坐标．

解答： 解：（1）．由函数的图象可知A=

- 1 2 -(- 3 2 )

2

=

1

2

，
k=

- 1 2 - 3 2

2

=-1，

T

2

=

2π

3

-

π

6

，T=π，∴ω=2，
当x=

π

6

时，y=-

1

2

，∴-

1

2

=

1

2

sin（2×

π

6

+φ）-1．
∵|φ|＜

π

2

，∴φ=

π

6

．
∴函数的解析式为：y=

1

2

sin（2x+

π

6

）-1．
（2）．由2x+

π

6

=kπ+

π

2

，k∈Z
解得：x=

π

6

+

kπ

2

，k∈Z
∴对称轴方程：x=

π

6

+

kπ

2

，k∈Z
由2x+

π

6

=kπ，k∈Z，解得x=-

π

12

+

kπ

2

，k∈Z．
对称中心坐标：（-

π

12

+

kπ

2

，-1），k∈Z．

点评：本题考点是三角函数的图象与性质，考查知道了三角函数图象上的特征求三角函数的解析式，以及根据三角函数的解析式求解三角函数的图象对称轴方程与对称中心坐标，是常规题型．