题目内容
 已知函数f(x)是定义在R上的偶函数,已知x≥0时,f(x)=-x+1.
已知函数f(x)是定义在R上的偶函数,已知x≥0时,f(x)=-x+1.(1)画出函数f(x)的图象;写出函数的解析式;
(2)根据图象,写出f(x)的单调区间;同时写出函数的值域.
考点:函数图象的作法,函数的值域,函数解析式的求解及常用方法,函数单调性的判断与证明
专题:函数的性质及应用
分析:(1)当x<0时,-x>0,利用函数为偶函数求得f(x)=f(-x)的解析式,可得f(x)在R上的解析式,如图所示.
(2)由函数f(x)的图象,数形结合求得f(x)的单调区间以及函数的值域.
(2)由函数f(x)的图象,数形结合求得f(x)的单调区间以及函数的值域.
解答:
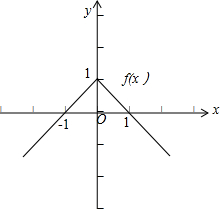 解:(1)由于函数f(x)是定义在R上的偶函数,已知x≥0时,f(x)=-x+1,
解:(1)由于函数f(x)是定义在R上的偶函数,已知x≥0时,f(x)=-x+1,
故当x<0时,-x>0,f(x)=f(-x)=-(-x)+1=x+1,∴f(x)=
,如图所示:
(2)由函数f(x)的图象可得,增区间为(-∞,0),减区间为[0,+∞),
函数的值域为(-∞,0].
 解:(1)由于函数f(x)是定义在R上的偶函数,已知x≥0时,f(x)=-x+1,
解:(1)由于函数f(x)是定义在R上的偶函数,已知x≥0时,f(x)=-x+1,故当x<0时,-x>0,f(x)=f(-x)=-(-x)+1=x+1,∴f(x)=
|
(2)由函数f(x)的图象可得,增区间为(-∞,0),减区间为[0,+∞),
函数的值域为(-∞,0].
点评:本题主要考查利用函数的奇偶性求函数的解析式,作函数的图象,函数的单调性和值域,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知函数f(x)=
,若存在x1,x2∈R且x1≠x2,使得f(x1)=f(x2)成立,则实数a的取值范围是( )
|
| A、a<0 | B、a≤0 |
| C、a<3 | D、0<a<3 |
已知f(x)=sin(2014x+
)+cos(2014x-
)的最大值为A,若存在实数x1,x2,使得对任意实数x总有f(x1)≤f(x)≤f(x2)成立,则A|x1-x2|的最小值为( )
| π |
| 6 |
| π |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知F是抛物线x2=4y的焦点,P是该抛物线上的动点,则线段PF中点轨迹方程是( )
A、x2=y-
| ||
B、x2=2y-
| ||
| C、x2=2y-2 | ||
| D、x2=2y-1 |
已知平面向量
=(2m+1,3),
=(2,m),且
与
反向,则|
|等于( )
| a |
| b |
| a |
| b |
| b |
A、
| ||||
B、
| ||||
C、
| ||||
D、2
|
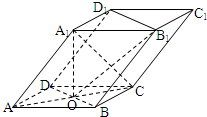 如图,四棱柱ABCD-A1B1C1D1的底面ABCD是正方形,O为底面中心,A1O⊥平面ABCD,AB=
如图,四棱柱ABCD-A1B1C1D1的底面ABCD是正方形,O为底面中心,A1O⊥平面ABCD,AB=