题目内容
在△ABC中，角A，B，C所对的边分别为a，b，c，已知
•
=3
•
．
（Ⅰ）求证tanB=3tanA；
（Ⅱ）若a2+b2-c2=
ab，求角A的大小．
| AB |
| AC |
| BA |
| BC |
（Ⅰ）求证tanB=3tanA；
（Ⅱ）若a2+b2-c2=
2
| ||
| 5 |
考点：余弦定理的应用,平面向量数量积的运算
专题：计算题,解三角形
分析：（Ⅰ）记AB=c，AC=b，BC=a由已知
•
=3
•
，可得bccosA=3cacosB由正弦定理化简得tanB=3tanA；
（Ⅱ）由余弦定理和已知得：cosC=
，即可求出1+tan2C=5解得tanC=2（tanC=-2舍去）结合（Ⅰ）即可求得角A的大小．
| AB |
| AC |
| BA |
| BC |
（Ⅱ）由余弦定理和已知得：cosC=
| ||
| 5 |
解答：
解（Ⅰ）记AB=c，AC=b，BC=a
∵
•
=3
•
．
∴bccosA=3cacosB
∴bcosA=3acosB
由正弦定理得：sinBcosA=3sinAcosB
∴
=3
∴tanB=3tanA．
（Ⅱ）∵a2+b2-c2=
ab
由余弦定理得：cosC=
∴1+tan2C=5
∴tanC=2（tanC=-2舍去）
tanC=tan[π-（A+B）]=-tan（A+B）=
=2
解得：tanA=-
（舍去），或tanA=1
∴A=
．
∵
| AB |
| AC |
| BA |
| BC |
∴bccosA=3cacosB
∴bcosA=3acosB
由正弦定理得：sinBcosA=3sinAcosB
∴
| sinB |
| cosB |
| sinA |
| cosA |
∴tanB=3tanA．
（Ⅱ）∵a2+b2-c2=
2
| ||
| 5 |
由余弦定理得：cosC=
| ||
| 5 |
∴1+tan2C=5
∴tanC=2（tanC=-2舍去）
tanC=tan[π-（A+B）]=-tan（A+B）=
| tanA+tanB |
| tanAtanB-1 |
解得：tanA=-
| 1 |
| 3 |
∴A=
| π |
| 4 |
点评：本题主要考察了余弦定理的应用，平面向量数量积的运算，考察了计算能力，属于中档题．
练习册系列答案
快捷英语周周练系列答案
相关题目
一个空间几何体的三视图如图所示，则该几何体的体积为（ ）
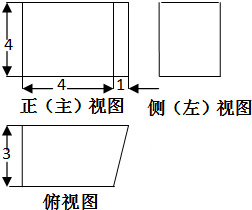
| A、12 | B、18 | C、27 | D、54 |
已知函数f（x）是定义在R上的偶函数，已知x≥0时，f（x）=-x+1．椭圆与双曲线
-
=1有相同的焦点且离心率为
，则椭圆的标准方程为（ ）
| x2 |
| 3 |
| y2 |
| 2 |
| 1 | ||
|
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
圆 C1：（x+2）2+（y-2）2=4和圆C2：（x-2）2+（y-5）2=16的位置关系是（ ）
| A、外离 | B、相交 | C、内切 | D、外切 |