题目内容
已知tanα和cosα是关于x的方程5x2-mx+4=0的两根，且α在第二象限
（1）求tanα及m的值；
（2）求
的值．
（1）求tanα及m的值；
（2）求
| 2sin2α-sinα•cosα+3cos2α |
| 1+sin2α |
考点：同角三角函数基本关系的运用
专题：三角函数的求值
分析：（1）由已知，得
，可求得sinα=
，又α在第二象限，于是可求得tanα及m的值；
（2）由（1）得：tanα=-
，将所求关系式中的“弦”化“切”即可得到答案．
|
| 4 |
| 5 |
（2）由（1）得：tanα=-
| 4 |
| 3 |
解答：
解：（1）由已知，得
，∴sinα=
，又α在第二象限，∴tanα=-
，m=-
；
（2）由（1）得：tanα=-
，∴原式=
=
．
|
| 4 |
| 5 |
| 4 |
| 3 |
| 29 |
| 3 |
（2）由（1）得：tanα=-
| 4 |
| 3 |
| 2tan2α-tanα+3 |
| 2tan2α+1 |
| 71 |
| 41 |
点评：本题考查同角三角函数基本关系的运用，（2）中“弦”化“切”是关键，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
已知函数f（x）的导函数f′（x），满足xf′（x）+2f（x）=
，且f（1）=1，则函数f（x）的最大值为（ ）
| 1 |
| x2 |
| A、0 | ||
B、
| ||
C、
| ||
| D、2e |
变量x，y满足约束条件
时，x-2y+m≤0恒成立，则实数m的取值范围为（ ）
|
| A、[0，+∞） |
| B、[1，+∞） |
| C、（-∞，3] |
| D、（-∞，0] |
一个空间几何体的三视图如图所示，则该几何体的体积为（ ）
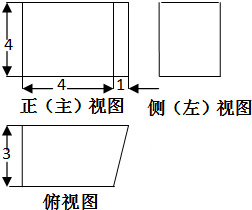
| A、12 | B、18 | C、27 | D、54 |
在等比数列{an}中，a7•a11=6，a4+a14=5，则
等于（ ）
| a20 |
| a10 |
A、
| ||||
B、
| ||||
C、
| ||||
D、-
|
原命题：“设a、b、c∈R，若ac2＞bc2则a＞b”和它的逆命题、否命题、逆否命题这四个命题中，真命题共有（ ）
| A、1个 | B、2个 | C、3个 | D、0个 |
已知函数f（x）是定义在R上的偶函数，已知x≥0时，f（x）=-x+1．