题目内容
已知直线x-y+1=0与圆x2+y2-4x-2y+m=0交于A、B两点
(1)求线段AB的垂直平分线的方程.
(2)若|AB|=2
,求m的值.
(1)求线段AB的垂直平分线的方程.
(2)若|AB|=2
| 2 |
考点:圆的一般方程
专题:计算题,直线与圆
分析:(1)由题意,线段AB的垂直平分线经过圆的圆心(2,1),斜率为-1,可得线段AB的垂直平分线的方程.
(2)利用|AB|=2
,求出圆心到直线的距离,利用点到直线的距离公式求出圆心到直线的距离,从而可求m的值.
(2)利用|AB|=2
| 2 |
解答:
解:(1)由题意,线段AB的垂直平分线经过圆的圆心(2,1),斜率为-1,
∴方程为y-1=-(x-2),即x+y-3=0;
(2)圆x2+y2-4x-2y+m=0可化为(x-2)2+(y-1)2=-m+5,
∵|AB|=2
,
∴圆心到直线的距离为
=
,
∵圆心到直线的距离为d=
=
,
∴
=
,
∴m=1
∴方程为y-1=-(x-2),即x+y-3=0;
(2)圆x2+y2-4x-2y+m=0可化为(x-2)2+(y-1)2=-m+5,
∵|AB|=2
| 2 |
∴圆心到直线的距离为
| -m+5-2 |
| 3-m |
∵圆心到直线的距离为d=
| |2-1+1| | ||
|
| 2 |
∴
| 3-m |
| 2 |
∴m=1
点评:本题考查点到直线的距离公式的应用,以及弦长公式的应用,比较基础.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
 在△ABC中,已知
在△ABC中,已知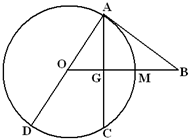 如图,已知AD为圆O的直径,直线BA与圆O相切于点A,直线OB与弦AC垂直并相交于点G,与弧AC相交于M,连接DC,AB=10,AC=12.
如图,已知AD为圆O的直径,直线BA与圆O相切于点A,直线OB与弦AC垂直并相交于点G,与弧AC相交于M,连接DC,AB=10,AC=12. 如图,已知BC为⊙O的直径,点A、F在⊙O上,AD⊥BC,垂足为D,BF交AD于E,且AE=BE.
如图,已知BC为⊙O的直径,点A、F在⊙O上,AD⊥BC,垂足为D,BF交AD于E,且AE=BE.